we know how combination with repetition when, having a set Ç with no elements, we form new sets, admitting repetitions with k elements, all belonging to the set Ç. The combination with repetition, also known as complete combination, is a type of grouping of combinatorial analysis.
The study of this type of grouping made it possible to develop a formula that facilitates the calculation of the combination with repetition. It is possible to relate the combination with repetition to a simple combination through a formula. The difference between the combination with repetition and the simple combination, as the name suggests, is that, in the former, the elements are assumed to be repeated in the subset, and in the latter, they are not.
Read too: What is arrangement with repetition?
What is the combination with repetition?

Combination with repetition or complete combination is one of several types of possible groupings studied in combinatorial analysis. On a
set with no elements, we will find the amount of unordered groupings that we can form with k elements, all belonging to the set, knowing that the same element can be chosen more than once.Here's a situation involving a combination with repetition: given a set {A, B, C, D}, we'll find all possible sets with two elements.
We know that, in a set, the order of the elements is not important, that is, {A, B} and {B, A} form the same set. Furthermore, as it is a combination with repetition, the same element of the set can be repeated, so the possible combinations are:
{A, A}; {B, B}; {C, C}; {D, D}; {A, B}; {A, C}; {A, D}; {B, C}; {B, D}; {CD}
Combination formula with repetition
In mathematical problems, the interest is often not in listing all possible sets, but in calculate the number of possible groupings, either for future probability calculations, or to generate some kind of statistics, or for another application. For this, we use a formula.
In a set with no elements taken from k in k, we calculate the complete combination or combination with repetition using the formula:
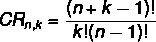
CR: combination with repetition
no: number of elements in the set
k: number of elements in each regrouping
Another important formula for calculating the combination with repetition is that relates a single match to a repeat match:

We use this formula to transform combination with repetition into a simple combination.
Step by step how to calculate the number of a combination with repetition
To calculate the number of possible combinations, allowing for repetitions, it is necessary to find the value of the no It's from k and substitute in the formula.
Example:
Using the previous example of the set, {A, B, C, D}, to calculate the combination with repetition of these terms taken from 2 to 2, we have:
1st We found the value of no it's from k:
no = 4
k = 2
2nd We replaced in the formula of combination with repetition:

See too: How to calculate simple arrangement?
solved exercises
Question 1 - The season that most heats up the chocolate sales market is Easter, thinking about it, a chocolate factory in the interior from Goiás, decided to innovate in the production of chocolate by creating Easter egg flavors, with Cerrado fruits such as Ingredients. The flavors created were dark chocolate with bacupari-do-cerrado, milk chocolate with pera-do-campo, white chocolate with murici, white chocolate with baru, and dark chocolate with buriti. A customer decided to go to this store to buy 1 easter egg for each of his 3 siblings. Knowing this, the number of different ways that this customer can choose these Easter eggs is:
A) 20
B) 22
C) 25
D) 32
E) 35
Resolution
Alternative E
Note that the order, in this case, is not important and also that the customer can choose to buy 2 or 3 easter eggs of the same flavor, which makes this problem related to the combination with repetitions.
There are five flavors available, and the customer will choose 3 easter eggs, so we have to:
no = 5
k = 3
Substituting in the formula of the combination with repetition, we have to:

Question 2 - A store offers 3 possible flavors of juices, they are: orange, lemon and pineapple. Knowing this, the number of different ways a customer can order 4 juices is:
A) 12
B) 15
C) 18
D) 20
E) 22
Resolution
Alternative B
There are 3 possible flavors and juice, and we will form sets with 4 flavors, in which case it is evident that the set admits repetitions, and that the order is not relevant, which makes this situation a combination with repetition. To calculate, we have to:
no = 3
k = 4

By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/combinacao-com-repeticao.htm

