Arithmetic Progression (P.A.)

THE Arithmetic Progression (P.A.) is a sequence of numbers where the difference between two consecutive terms is always the same. This constant difference is called the P.A.

Thus, from the second element of the sequence onwards, the numbers that appear are the result of the sum of the constant with the value of the previous element.

This is what differentiates it from the geometric progression (PG), because in this one, the numbers are multiplied by the ratio, while in the arithmetic progression, they are added.

Arithmetic progressions can have a fixed number of terms (finite P.A.) or an infinite number of terms (infinite P.A.).

To indicate that a sequence continues indefinitely we use ellipses, for example:

• the sequence (4, 7, 10, 13, 16, ...) is an infinite P.A.
• the sequence (70, 60, 50, 40, 30, 20, 10) is a finite P.A.

Each term of a P.A. is identified by the position it occupies in the sequence and to represent each term we use a letter (usually the letter The) followed by a number indicating its position in the sequence.

For example, the term The₄ in P.A (2, 4, 6, 8, 10) is the number 8, as it is the number that occupies the 4th position in the sequence.

Classification of a P.A.

According to the ratio value, arithmetic progressions are classified into:

• Constant: when the ratio is equal to zero. For example: (4, 4, 4, 4, 4...), where r = 0.
• Growing: when the ratio is greater than zero. For example: (2, 4, 6, 8,10...), where r = 2.
• descending: when the ratio is less than zero (15, 10, 5, 0, - 5,...), where r = - 5

P.A. Properties

1st property:

In a finite P.A., the sum of two terms equidistant from the extremes is equal to the sum of the extremes.

Example

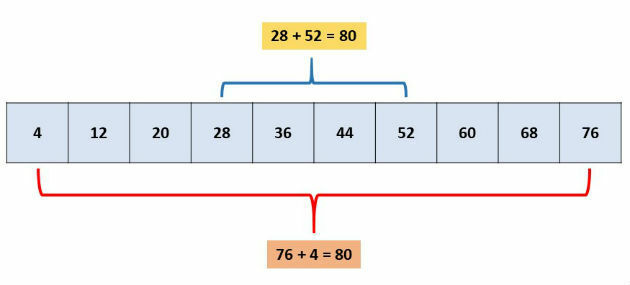
2nd property:

Considering three consecutive terms of a P.A., the middle term will be equal to the arithmetic mean of the other two terms.

Example

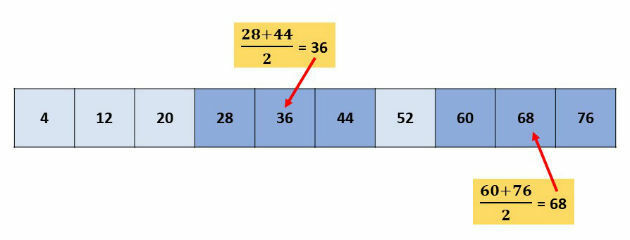
3rd property:

In a finite P.A. with odd number of terms, the central term will be equal to the arithmetic mean between terms equidistant from it. This property derives from the first.

General Term Formula

Where,

an: term we want to calculate
a1: first term of P.A.
n: position of the term we want to discover
r: reason

Formula explanation

As the ratio of a P.A. is constant, we can calculate its value from any consecutive terms, that is:

Therefore, we can find the value of the second term of the P.A. by doing:

To find the third term we will use the same calculation:

Replacing the value of a₂, which we found earlier, we have:

If we follow the same reasoning, we can find:

Observing the results found, we note that each term will be equal to the sum of the first term with the ratio multiplied by the previous position.

This calculation is expressed through the formula of the general term of the P.A., which allows us to know any element of an arithmetic progression.

Example

Calculate the 10th term of the P.A.: (26, 31, 36, 41, ...)

Solution

First, we must identify that:

The₁ = 26
r = 31 - 26 = 5
n = 10 (10th term).

Substituting these values ​​in the formula of the general term, we have:

The_no = the₁ + (n - 1). r
The₁₀ = 26 + (10-1). 5
The₁₀ = 26 + 9 .5
The₁₀ = 71

Therefore, the tenth term of the indicated arithmetic progression is equal to 71.

General term formula from any k term

Often, to define any generic term, which we call an, we don't have the first term a1, but we know any other term, which we call ak.

We can use the general term formula from any k term:

Note that the only difference was the change from index 1 in the first formula to k in the second.

Being,

an: the n-th term of the P.A. (a term in any n position)
ak: the k-th term of a P.A. (a term at any k position)
r: the reason

Sum of Terms of a P.A.

To find the sum of terms of a finite P.A., just use the formula:

Where,

s_no: sum of the first n terms of P.A.
The₁: first term of P.A.
The_no: occupies the nth position in the sequence (a term in position n)
no: term position

Also read about PA and PG.

Exercise solved

Exercise 1

PUC/RJ - 2018

Knowing that the numbers in the sequence (y, 7, z, 15) are in arithmetic progression, what is the sum y + z worth?

a) 20
b) 14
c) 7
d) 3.5
e) 2

See Answer

To find the value of z, we can use the property that says that when we have three consecutive terms the middle term will be equal to the arithmetic mean of the other two. So we have:

If z is equal to 11, then the ratio will be equal to:

r = 11 - 7 = 4

This way, y will be equal to:

y = 7 - 4 = 3

Therefore:

y+z = 3 + 11 = 14

Alternative: b) 14

Exercise 2

IFRS - 2017

In the figure below, we have a sequence of rectangles, all of height a. The base of the first rectangle is b and of subsequent rectangles it is the value of the base of the previous one plus a unit of measure. Thus, the base of the second rectangle is b+1 and the third is b+2 and so on.

Consider the statements below.

I - The sequence of the rectangle areas is an arithmetic progression of ratio 1.
II - The sequence of the rectangle areas is an arithmetic progression of ratio a.
III - The sequence of the areas of the rectangles is a geometric progression of ratio a.
IV - The area of ​​the nth rectangle (A_no) can be obtained by formula A_no = a. (b + n - 1).

Check the alternative that contains the correct statement(s).

there.
b) II.
c) III.
d) II and IV.
e) III and IV.

See Answer

Calculating the area of ​​the rectangles, we have:

A = a. B
THE₁ = a. (b + 1) = a. b + a
THE₂ = a. (b + 2) = a. B. + 2nd
THE₃ = a. (b + 3) = a. b + 3a

From the expressions found, we note that the sequence forms a P.A. of ratio equal to The. Continuing the sequence, we will find the area of ​​the nth rectangle, which is given by:

THE_no= a. b + (n - 1) .a
THE_no = a. b + a. at

putting the The in evidence, we have:

THE_no = a (b + n - 1)

Alternative: d) II and IV.

Exercise 3

UERJ

Admit the holding of a football championship in which the warnings received by athletes are represented only by yellow cards. These cards are converted into fines, according to the following criteria:

• The first two cards received do not generate fines;
• The third card generates a fine of R$500.00.
• The following cards generate fines whose values ​​are always increased by R$500.00 in relation to the value of the previous fine.

The table shows the fines related to the first five cards applied to an athlete.

Consider an athlete who received 13 yellow cards during the championship. The total amount, in reais, of the fines generated by all these cards is:

a) 30,000
b) 33 000
c) 36 000
d) 39 000

See Answer

Correct answer: b) 33 000

As of the third yellow card, the amount of the fine increases in a P.A. with a ratio of R$500.00. Considering the first term, a1, with the value of the third card, R$500.00.

To determine the total amount of the fines, we must use the formula of the sum of the terms of the P.A.

As the athlete has 13 yellow cards, but the first two do not generate fines, we will make a P.A. of 13-2 terms, that is, 11 terms.

Thus, we have the following values:

a1 = 500
n = 11
r = 500

To find the value of the nth term, a11, we use the general term formula.

an = a1 + (n-1).r
a21 = 500 +(11-1) x 500
a21 = 500 + 10 x 500
a21 = 5500

Applying the formula of the sum of terms of a P.A.

Solve more exercises in:

Arithmetic Progression - Exercises

Learn more by also reading:

• Numerical Sequence
• Geometric progression
• Geometric Progression - Exercises
• Math Formulas