The determinant is a number associated with a square matrix. This number is found by performing certain operations with the elements that make up the matrix.
We indicate the determinant of a matrix A by det A. We can still represent the determinant by two bars between the elements of the matrix.
1st Order Determinants
The determinant of a matrix of Order 1 is the same as the matrix element itself, as it has only one row and one column.
Examples:
det X = |8| = 8
det Y = |-5| = 5
2nd Order Determinants
At matrices Order 2 or 2x2 matrix are those that have two rows and two columns.
The determinant of a matrix of this type is calculated by first multiplying the constant values in the diagonals, one principal and one secondary.
Then subtracting the results obtained from that multiplication.
Examples:
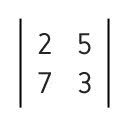
3 * 2 - 7 * 5 = 6 - 35 = -29
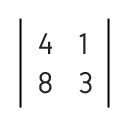
3 * 4 - 8 * 1 = 12 - 8 = 4
3rd Order Determinants
Order 3 matrices or 3x3 matrix are those that have three rows and three columns:
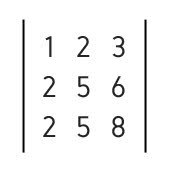
To calculate the determinant of this type of matrix, we use the
Sarrus' Rule, which consists of repeating the first two columns right after the third:
Then, we follow the following steps:
1) We calculate diagonal multiplication. To do so, we draw diagonal arrows that facilitate the calculation.
The first arrows are drawn from left to right and correspond to the main diagonal:

1 * 5 * 8 = 40
2 * 6 * 2 = 24
3 * 2 * 5 = 30
2) We calculate the multiplication on the other side of the diagonal. So we draw new arrows.
Now the arrows are drawn from right to left and correspond to the secondary diagonal:

2 * 2 * 8 = 32
1 * 6 * 5 = 30
3 * 5 * 2 = 30
3) We add each one of them:
40 + 24 + 30 = 94
32 + 30 + 30 = 92
4) We subtract each of these results:
94 - 92 = 2
read Matrices and Determinants and, to understand how to calculate matrix determinants of order equal to or greater than 4, read Laplace's Theorem.
Exercises
1. (UNITAU) The determinant value (image below) as a product of 3 factors is:
a) abc.
b) a (b + c) c.
c) a (a - b) (b - c).
d) (a + c) (a - b) c.
e) (a + b) (b + c) (a + c).

Alternative c: a (a - b) (b - c).
2. (UEL) The sum of the determinants indicated below is equal to zero (image below)
a) whatever the actual values of a and b
b) if and only if a = b
c) if and only if a = - b
d) if and only if a = 0
e) if and only if a = b = 1
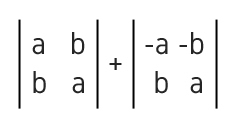
Alternative: a) whatever the real values of a and b
3. (UEL-PR) The determinant shown in the following figure (image below) is positive whenever
a) x > 0
b) x > 1
c) x d) x e) x > -3
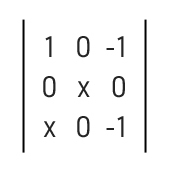
Alternative b: x > 1