Kinematics: Commented and Solved Exercises

THE kinematics it is the area of ​​Physics that studies movement without, however, considering the causes of this movement.

In this field, we mainly study uniform rectilinear motion, uniformly accelerated rectilinear motion, and uniform circular motion.

Take advantage of the commented questions to clear all your doubts about this content.

Solved Exercises

question 1

(IFPR - 2018) A vehicle travels at 108 km/h on a highway, where the maximum speed allowed is 110 km/h. By tapping the driver's cell phone, he recklessly diverts his attention to the phone over 4s. The distance covered by the vehicle during the 4 s in which it moved without the driver's attention, in m, was equal to:

a) 132.
b) 146.
c) 168.
d) 120.

See Answer

Correct alternative: d) 120

Considering that the vehicle speed remained constant during the 4s, we will use the hourly equation of the uniform movement, that is:

y = y₀ + v.t

Before replacing the values, we need to transform the unit of speed from km/h to m/s. To do this, just divide by 3.6:

v = 108: 3.6 = 30 m/s

Replacing the values, we find:

y - y₀ = 30. 4 = 120 m

To learn more, see also: Uniform Movement

question 2

(PUC/SP - 2018) Through a PVC reduction glove, which will be part of a pipe, 180 liters of water will pass per minute. The inner diameters of this sleeve are 100 mm for the water inlet and 60 mm for the water outlet.

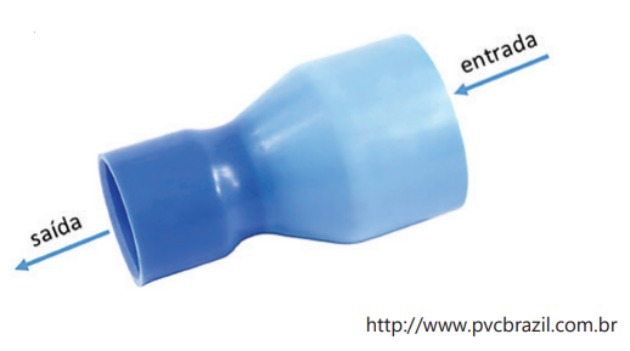
Determine, in m/s, the approximate velocity at which the water leaves this glove.

a) 0.8
b) 1.1
c) 1.8
d) 4.1

See Answer

Correct alternative: b) 1.1

We can calculate the flow in the pipeline by dividing the liquid volume by the time. However, we must transfer the units to the international system of measurements.

Thus, we will have to transform minutes into seconds and liters into cubic meters. For this, we will use the following relationships:

• 1 minute = 60 s
• 1 l = 1 dm³ = 0.001 m³⇒ 180 l = 0.18 m³

Now, we can calculate the flow (Z):

To find the value of the leaving water velocity, let's use the fact that the flow is equal to the area of ​​the pipe multiplied by the velocity, that is:

Z = A. v

To do this calculation, we first need to know the output area value, and for that we will use the formula for the area of ​​a circle:

A = π. R²

We know that the output diameter is equal to 60 mm, so the radius will equal 30 mm = 0.03 m. Considering the approximate value of π = 3.1 and substituting these values, we have:

A=3.1. (0,03)² = 0.00279 m²

Now, we can find the velocity value by substituting the flow and area value:

To learn more, see also: Physics Formulas

question 3

(PUC/RJ - 2017) From the ground, a ball is launched vertically with velocity v and reaches a maximum height h. If the throw speed is increased by 3v, the new maximum final height reached by the ball will be: (Neglect air resistance)

a) 2h
b) 4h
c) 8 am
d) 9 am
e) 16h

See Answer

Correct alternative: e) 16h

The height reached by the ball can be calculated using the Torricelli equation, ie:

v² = v₀² - 2.g.h

The acceleration due to gravity is negative as the ball is rising. Also, the speed when the ball reaches its maximum height is equal to zero.

Thus, in the first situation, the value of h will be found by doing:

In the second situation, the speed was increased by 3v, that is, the launch speed was changed to:

v₂ = v + 3v = 4v

Thus, in the second situation, the height reached by the ball will be:

Alternative: e) 16h

To learn more, see also: Uniformly Varied Rectilinear Movement

question 4

(UECE - 2016 - 2nd phase) Consider a stone in free fall and a child on a carousel that rotates with constant angular velocity. About the movement of the stone and the child, it is correct to state that

a) the acceleration of the stone varies and the child rotates with zero acceleration.
b) the stone falls with zero acceleration and the child rotates with constant acceleration.
c) the acceleration in both is zero.
d) both undergo constant modulus accelerations.

See Answer

Correct alternative: d) both undergo constant modulo accelerations.

Both velocity and acceleration are vector quantities, that is, they are characterized by magnitude, direction and direction.

For a quantity of this type to undergo a variation, it is necessary that at least one of these attributes undergo modifications.

When a body is in free fall, its velocity module varies uniformly, with constant acceleration equal to 9.8 m/s² (acceleration of gravity).

In the carousel, the velocity module is constant, however, its direction is varying. In this case, the body will have a constant acceleration and that it points to the center of the circular path (centripetal).

See too: Exercises on Uniform Circular Movement

question 5

(UFLA - 2016) A stone was thrown vertically upwards. As it is rising, the
a) speed decreases and acceleration decreases
b) speed decreases and acceleration increases
c) velocity is constant and acceleration decreases
d) speed decreases and acceleration is constant

See Answer

Correct alternative: d) speed decreases and acceleration is constant

When a body is launched vertically upwards, close to the surface of the earth, it suffers the action of a gravitational force.

This force gives you a constant acceleration of modulus equal to 9.8 m/s², vertical direction and down direction. In this way, the velocity module decreases until it reaches the value equal to zero.

question 6

(UFLA - 2016) The scaled figure shows the displacement vectors of an ant, which, leaving point I, reached point F, after 3 min and 20 s. The modulus of the mean velocity vector of the ant's movement in this path was:

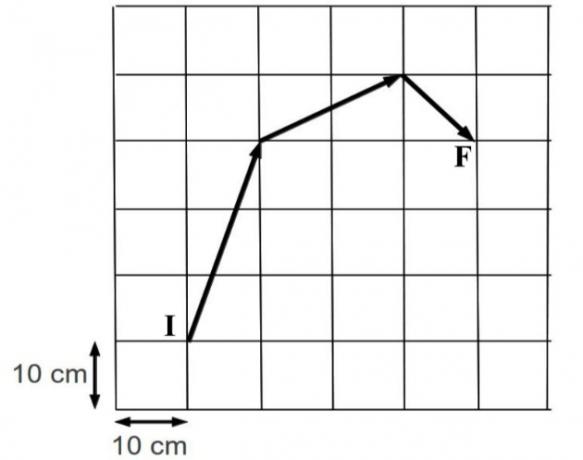
a) 0.15 cm/s
b) 0.25 cm/s
c) 0.30 cm/s
d) 0.50 cm/s

See Answer

Correct alternative: b) 0.25 cm/s

The modulus of the mean velocity vector is found by calculating the ratio between the modulus of the displacement vector and the time.

To find the displacement vector, we must connect the start point to the end point of the ant's trajectory, as shown in the image below:

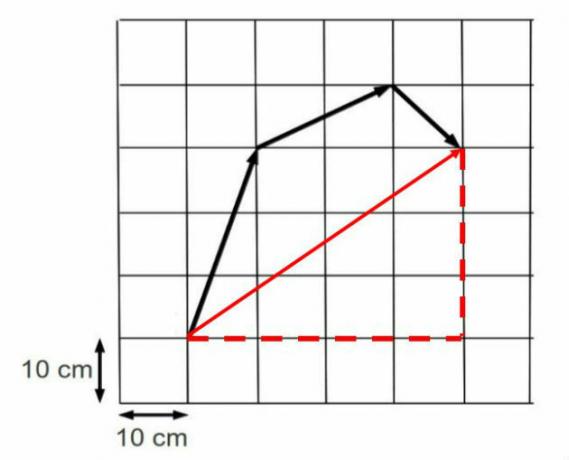
Note that its modulus can be found by doing Pythagoras' theorem, since the length of the vector is equal to the hypotenuse of the indicated triangle.

Before we find the speed, we must transform the time from minutes to seconds. With 1 minute being equal to 60 seconds, we have:

t = 3. 60 + 20 = 180 + 20 = 200 s

Now, we can find the speed module by doing:

See too: kinematics

question 7

(IFMG - 2016) Due to a serious accident that occurred in an ore tailings dam, a first wave of these tailings, faster, invaded a hydrographic basin. An estimate for the size of this wave is 20 km long. An urban stretch of this hydrographic basin is about 25 km long. Assuming in this case that the average speed at which the wave passes through the river channel is 0.25 m/s, the total time of passage of the wave through the city, counted from the arrival of the wave in the urban stretch, is in:

a) 10 hours
b) 50 hours
c) 80 hours
d) 20 hours

See Answer

Correct alternative: b) 50 hours

The distance covered by the wave will be equal to 45 km, that is, the measure of its extension (20 km) plus the extension of the city (25 km).

To find the total passage time we will use the average speed formula, like this:

However, before replacing the values, we must transform the speed unit to km/h, thus, the result found for the time will be in hours, as indicated in the options.

Making this transformation we have:

v_m = 0,25. 3.6 = 0.9 km/h

Substituting the values ​​in the average speed formula, we find:

question 8

(UFLA - 2015) Lightning is a complex natural phenomenon, with many aspects still unknown. One of these aspects, barely visible, occurs at the beginning of the discharge propagation. The discharge from the cloud to the ground starts in a process of ionization of the air from the base of the cloud and propagates in stages called consecutive steps. A high-speed frame-per-second camera identified 8 steps, 50 m each, for a specific discharge, with time interval recordings of 5.0 x 10^-4 seconds per step. The average velocity of propagation of the discharge, in this initial stage called the stepped leader, is of
a) 1.0 x 10^-4 m/s
b) 1.0 x 10⁵ m/s
c) 8.0 x 10⁵ m/s
d) 8.0 x 10^-4 m/s

See Answer

Correct alternative: b) 1.0 x 10⁵ m/s

The average propagation speed will be found by doing:

To find the value of Δs, just multiply 8 by 50 m, as there are 8 steps with 50 m each. Thus:

Δs = 50. 8 = 400 m.

As the interval between each step is 5.0. 10^-4 s, for 8 steps the time will be equal to:

t = 8. 5,0. 10^-4 = 40. 10^-4 = 4. 10^-3 s

You may also be interested in:

• Torricelli Equation
• kinematics formulas
• evenly varied movement
• Uniform Rectilinear Movement
• Uniform Movement - Exercises
• Average Speed ​​Exercises