Power is a measure of how fast a task is performed, or how many tasks are performed in a given time interval.
In physics, the concept of power relates the amount of energy that is consumed, or supplied, to perform these tasks, and the time that was used.
If two machines do the same job and one of them does it in half the time, the faster is the more powerful. If two machines work the same amount of time, and one of them produces twice as much, the machine that produced the most is the most powerful.
The power is the result of the division between the work and the time interval used to carry out this work, being a scalar quantity, that is, it is not necessary to define direction and direction.
Average power formula
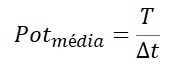
Where:
T is work, measured in J (joules);, measured in s (seconds).
As the amount of work, that is, energy, used or delivered, can vary over a period of time, the formula above gives the average power.
power unit
In the international system (SI), the unit of work is the joule (J) and the time is the second (s). That's why the unit of power is J/s, a measure so important that it was given a special name, the watt (W), in honor of James Watt, inventor, mathematician, and engineer. Considered by many to be the precursor of the industrial revolution, James Watt perfected the steam engine and, later, patented his own engine, in addition to many other contributions.
Another concept developed by James Watt was HP (Horse-Power), or CV (horsepower).
It is common to come across other ways of representing power, such as the multiple kW(1,000 W) and MW(1,000,000 W), commonly used in electrical energy supply.
In foot-pound-seconds, 1 watt is expressed as:
Power of a constant force in a displacement
Potency is expressed by:
A force F, performs work on a body, moving it from point A to point B. The work performed by force F when moving the body can be calculated as follows:
Where:
F is a constant force, measured in Newtons (N).
d is the displacement, measured in meters (m).
cos θ is the cosine of angle θ. (angle formed between the directions of force and movement)
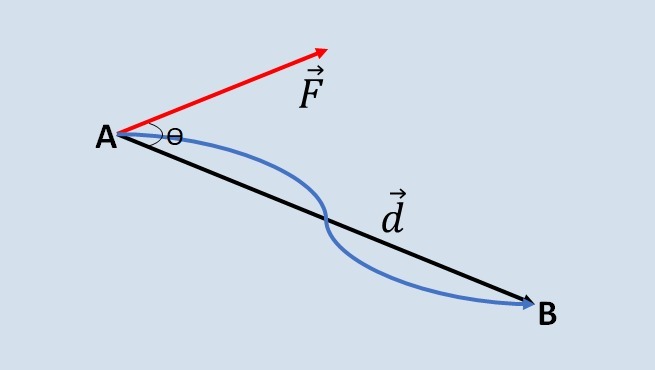
Power of a force as a function of average speed
As the average speed is the displacement divided by the time, according to the relation:
Substituting the work's previous equation, we have:
instantaneous power
The potency is the result of dividing the work and the amount of time used to perform that work. If we take a very small time interval, tending towards zero, we have the instantaneous power.
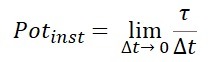
Where,
means that the division will be done with a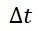 
very close to zero.
Performance
The efficiency of a machine or device is the ratio between the power actually used and the power it received. This useful power is the usable part, it is the power that was received minus that which was dissipated.
A device or machine that receives an amount of power cannot fully transform it into work, a part is lost due to friction, in the form of heat, noise and other processes.
Potu = Potr - Potd
Where:
Potu is the useful power;
foal is the received power;
Potd is the dissipated power.
Income formula
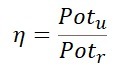
Where,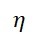
is the income;
Potu is the useful power;
foal is the received power.
Another way of expressing yield is to substitute the expression of useful power for yield.
Yield is always less than 100%. To understand why this happens, it is necessary to see that in the formula, the useful power, which is in the numerator, is always less than the received power, as there is always dissipation.
As it is a division between quantities of the same unit, the yield does not have a measurement unit, as they are canceled in the division. We say it is a dimensionless quantity and it is common to express it as a percentage.
The idea of yield can be extended to electrical, thermal and mechanical machines.
Learn more about performance with Carnot Cycle.
Exercises
question 1
A ship that will transport an order of cars docks to load it. The vehicles are in containers and have an approximate mass of 4000 kg each. To move them from the harbor to the ship's deck, a crane lifts them to a height of 30 m. Each operation of lifting a container lasts 5 min.
Calculate the power used by the crane to perform this task. Consider the acceleration of gravity g, equal to 10 m/s².
Resolution:
Since the average power is work divided by time, and time is already provided by the problem, we need to determine work.
Data:
m = 4000 kg
height = 30 m
t = 5 min = 5 x 60 s = 300 s
g = 10 m/s².
Crane work will be given by weight force.
Thus,
The power used will be 4 kW.
question 2
On a road, a car moves at a constant speed of 40 m/s. To perform this movement, apply a constant horizontal force in the same direction as the velocity. The engine produces an output of 80 kW. What is the intensity of the applied force?
Resolution:
We can determine strength through its relationship to power and speed.
Data:
Vm = 40 m/s
Pot = 80 kW
The power of a constant force is given by the product of the force by the velocity and by the cosine of the angle formed between them. As in this case force and velocity are in the same direction and direction, the angle θ is zero and cosine is 1.
Pot = F. Vm. cos θ
Pot = F.Vm. cos 0
Pot = F. Vm. 1
Isolating F and replacing the values,
The intensity of the applied force will be 20 kN.
question 3
(Fuvest-SP). A conveyor belt transports 15 cases of beverages per minute from an underground warehouse to the ground floor. The treadmill has a length of 12 m, an inclination of 30º from the horizontal and moves with constant speed. The boxes to be transported are already placed with the speed of the conveyor. If each box weighs 200 N, the motor that drives this mechanism must provide the power of:
a) 20W
b) 40W
c) 300W
d) 600W
e) 1800W
Resolution:
Power is given by the relationship between work and time used, in seconds.
Data:
t = 1 min = 60 s
Belt length = 12 m
slope = 30°
P = 200 N per box
With 15 boxes, we have 200 N x 15 = 3000 N.
So P = 3000 N, therefore mg = 3000 N.
As the work of the gravitational force is given by T = m.g.h, we need to determine the height.
At height h, the mat forms a right-angled triangle 30º in relation to the horizontal. So, to determine h, we will use the sine of 30º.
From trigonometry, we know that sine 30° = 1/2.
The work will be given by:
To determine the potency, just divide the work by the time.
The answer, therefore, is the letter c.
You for being interested in:
Electric power
work and energy
Physics formulas
