Kepler's Laws are three laws, proposed in the 17th century, by the German astronomer and mathematician Johannes Kepler (1571-1630), in the work New Astronomy (1609).
They describe the movements of the planets, following heliocentric models, that is, the Sun at the center of the solar system.
Kepler's Laws: Summary
Below are Kepler's three Laws on planetary motion:
Kepler's First Law
The 1st Law describes the orbits of the planets. Kepler proposed that the planets revolve around the Sun in an elliptical orbit, with the Sun at one of the focuses.
In this Law, Kepler corrects the model proposed by Copernicus which described how to circle the orbital motion of the planets.
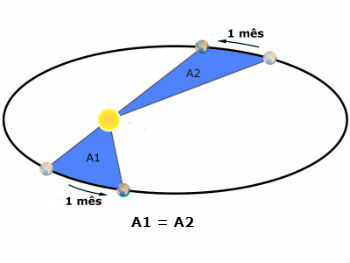
Kepler's Second Law
Kepler's 2nd law ensures that the segment (vector ray) that joins the sun to a planet sweeps across equal areas at equal time intervals.
A consequence of this fact is that the planet's speed along its orbital trajectory is different.
Being larger when the planet is closer to its perihelion (smallest distance between the planet and the Sun) and smaller when the planet is close to its aphelion (greater distance from the planet to Sun).
Kepler's Third Law
Kepler's 3rd law indicates that the square of each planet's period of revolution is proportional to the cube of the average radius of its orbit.
Therefore, the farther the planet is from the sun, the longer it will take to complete the translation.
Mathematically, Kepler's third law is described as follows:
Where:
T: corresponds to the planet's translation time
r: the average radius of the planet's orbit
K: constant value, that is, it has the same value for all bodies that orbit around the Sun. The constant K depends on the value of the Sun's mass.
Therefore, the ratio between the squares of the planets' periods of translation and the cubes of the respective average radii of the orbits will always be constant, as shown in the table below:

Kepler's Laws and Universal Gravitation
Kepler's Laws describe the motion of the planets, without regard for their causes.
Isaac Newton by studying these Laws, he identified that the speed of planets along the trajectory is variable in value and direction.
To explain this variation, he identified that there were forces acting on the planets and the Sun.
He deduced that these forces of attraction depend on the mass of the bodies involved and their distances.
Called the Universal Gravitation Law, its mathematical expression is:
Being,
F: gravitational force
G: universal gravitation constant
M: mass of the sun
m: planet mass
Watch the video about the mathematician's thoughts that led him to create Kepler's Laws:
Solved Exercises
1) Enem - 2009
The space shuttle Atlantis was launched into space with five astronauts on board and a new camera, which would replace one damaged by a short circuit in the Hubble telescope. After entering orbit at 560 km high, the astronauts approached Hubble. Two astronauts left Atlantis and headed for the telescope. Opening the access door, one of them exclaimed: "This telescope has a large mass, but the weight is small."
Considering the text and Kepler's laws, it can be said that the phrase said by the astronaut
a) is justified because the size of the telescope determines its mass, while its small weight is due to the lack of action of gravity acceleration.
b) is justified by verifying that the telescope's inertia is large compared to its own, and that the telescope's weight is small because the gravitational attraction created by its mass was small.
c) is not justified, because the evaluation of the mass and weight of objects in orbit is based on Kepler's laws, which do not apply to artificial satellites.
d) it is not justified, because the force-weight is the force exerted by the earth's gravity, in this case, on the telescope and is responsible for keeping the telescope itself in orbit.
e) it is not justified, as the action of the force-weight implies the action of a counter-reaction force, which does not exist in that environment. The telescope's mass could be judged simply by its volume.
Alternative d: it is not justified, because the force-weight is the force exerted by the Earth's gravity, in this case, on the telescope and is responsible for keeping the telescope itself in orbit.
2) UFRGS - 2011
Consider the average radius of Jupiter's orbit around the Sun equal to 5 times the average radius of Earth's orbit.
According to Kepler's 3rd Law, the period of Jupiter's revolution around the Sun is approximately
a) 5 years
b) 11 years
c) 25 years
d) 110 years
e) 125 years
Alternative b: 11 years
3) Enem - 2009
In line with an ancient tradition, the Greek astronomer Ptolemy (100-170 d. C.) affirmed the thesis of geocentrism, according to which the Earth would be the center of the universe, with the Sun, Moon and planets rotating around it in circular orbits. Ptolemy's theory reasonably solved the astronomical problems of his day. Several centuries later, the Polish cleric and astronomer Nicolas Copernicus (1473-1543), finding inaccuracies in Ptolemy's theory, formulated the theory. of heliocentrism, according to which the Sun should be considered the center of the universe, with the Earth, Moon and planets circling around from him. Finally, the German astronomer and mathematician Johannes Kepler (1571-1630), after studying the planet Mars for about thirty years, found its orbit to be elliptical. This result was generalized to the other planets.
Regarding the scholars cited in the text, it is correct to state that
a) Ptolemy presented the most valuable ideas, as they are older and more traditional.
b) Copernicus developed the theory of heliocentrism inspired by the political context of King Sun.
c) Copernicus lived at a time when scientific research was freely and widely encouraged by the authorities.
d) Kepler studied the planet Mars to meet Germany's economic and scientific expansion needs.
e) Kepler presented a scientific theory that, thanks to the applied methods, could be tested and generalized.
Alternative e: Kepler presented a scientific theory that, thanks to the applied methods, could be tested and generalized.
To learn more, read also:
- Johannes Kepler
- Translation Movement
- rotation movement
- heliocentrism
- Geocentrism
- Physics Formulas