In Mathematics, sets represent the gathering of various objects and the operations performed with sets are: union, intersection and difference.
Use the 10 questions below to test your knowledge. Use the commented resolutions to clear your doubts.
question 1
Consider the sets
A = {1, 4, 7}
B = {1, 3, 4, 5, 7, 8}
It is correct to say that:
a) A B
b) The B
c) B THE
d) B THE
Correct alternative: b) A B.
a) WRONG. There are elements of B that do not belong to set A. Therefore, we cannot say that A contains B. The correct statement would be B THE.
b) CORRECT. Note that all elements of A are also elements of B. Therefore, we can say that A is contained in B, A is part of B, or that A is a subset of B.
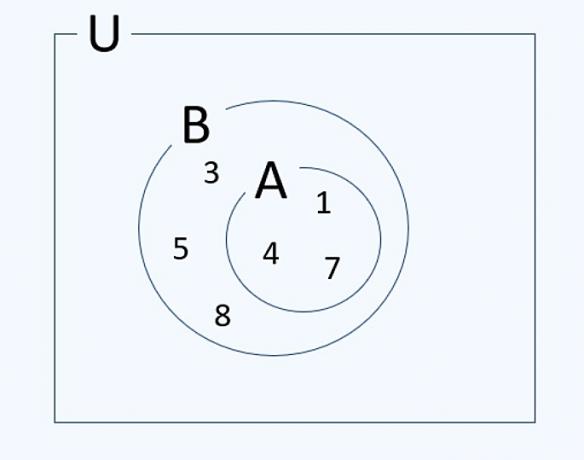
c) WRONG. There is no element of A that does not belong to set B. Therefore, we cannot say that B does not contain A.
d) WRONG. Since A is a subset of B, then the intersection of sets A and B is the set A itself: B A = A
question 2
Look at the following sets and mark the correct alternative.
A = {x|x is a positive multiple of 4}
B = {x|x is an even number and 4 x
16}
a) 145 THE
b) 26 A and B
c) 11 B
d) 12 A and B
Correct alternative: d) 12 A and B
The sets of the question are represented by their formation laws. Thus, set A is formed by positive multiples of 4, that is, A = {0, 4, 8, 12, 16, 20, 24,…} and set B gathers even numbers greater than or equal to 4 and less than 16. Therefore, B = {4, 6, 8, 10, 12, 14}.
Analyzing the alternatives, we have:
a) WRONG. 145 is a number ending in 5 and therefore is a multiple of 5.
b) WRONG. 26, despite being an even number, is greater than 16 and, therefore, is not part of set B.
c) WRONG. 11 is not an even number, but a prime number, that is, it is only divisible by 1 and itself.
d) CORRECT. 12 belongs to sets A and B as it is a multiple of 4 and is an even number greater than 4 and less than 16.
question 3
What is the possible law of formation of the set A = {2, 3, 5, 7, 11}?
a) A = {x|x is a symmetric number and 2 b) A = {x|x is a prime number and 1 c) A = {x|x is a positive odd number and 1 d) A = {x| x is a natural number less than 10}
Correct alternative: b) A = {x|x is a prime number and 1
a) WRONG. Symmetric numbers, also called opposites, appear at the same distance on the number line. For example, 2 and - 2 are symmetric.
b) CORRECT. The set presented is of prime numbers, with 2 being the smallest existing prime number and also the only one that is even.
c) WRONG. Although most numbers are odd there is the number 2 in the set, which is even.
d) WRONG. Although all numbers are natural, the set contains the number 11, which is greater than 10.
question 4
The union of sets A = {x|x is a prime number and 1
a) A B = {1,2,3,5.7}
b) The B = {1,2,3,5.7}
c) The B = {1,2,3,5.7}
gives B = {1,2,3,5.7}
Correct alternative: d) A B = {1, 2, 3, 5, 7}
For the set A = {x|x is a prime number and 1
A = {2, 3, 5, 7}
B = {1, 3, 5, 7}
a) WRONG. A does not contain B, as element 1 is not part of A.
b) WRONG. A is not contained in B, as element 2 is not part of B.
c) WRONG. A does not belong to B, as sets have a distinct element.
d) CORRECT. The union of sets corresponds to the joining of the elements that compose them and is represented by the symbol .
Therefore, the union of A = {2, 3, 5, 7} and B = {1, 3, 5, 7} is A U B = {1, 2, 3, 5, 7}.
question 5
Plot the sets A = {-3, - 1, 0, 1, 6, 7}, B = {-4, 1, 3, 5, 6, 7} and C = {-5, - 3, 1, 2, 3, 5} in the Venn diagram and then determine:

a) A B
b) C B
c) C - A
d) B (THE
Ç)
Right answer:
a) {1, 6, 7};
b) {-5, -4, -3, 1, 2, 3, 5, 6, 7};
c) {-5, 2, 3, 5} and
d) {1, 3, 5, 6, 7}.
Distributing the elements of the sets in the Venn diagram, we have:

When performing operations with the given sets, we have the following results:
a) A B = {1, 6, 7}
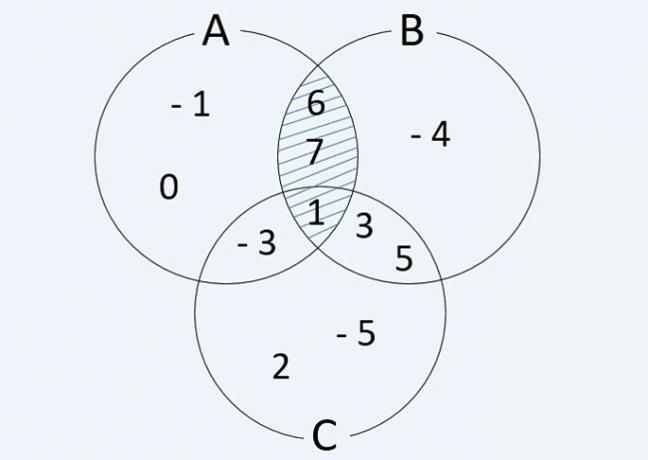
b) C B = {-5, -4, -3, 1, 2, 3, 5, 6, 7}
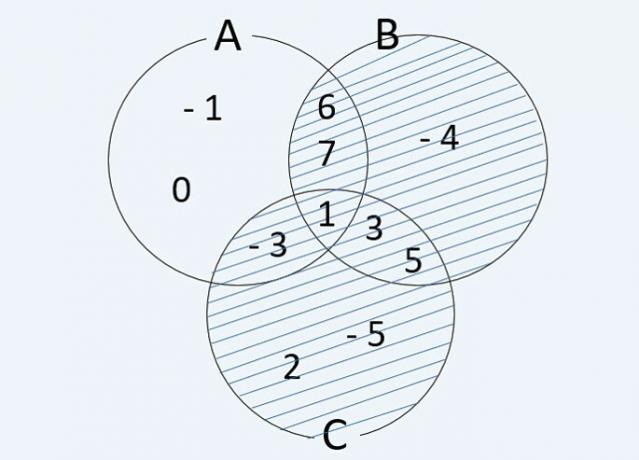
c) C - A = {-5, 2, 3, 5}

d) B (THE
C) = {1, 3, 5, 6, 7}

question 6
Note the hatched area of the figure and mark the alternative that represents it.

a) C (THE
B)
b) C - (A B)
c) C (A - B)
d) C (THE
B)
Correct answer: b) C – (A B)
Note that the hatched area represents elements that do not belong to sets A and B. Therefore, it is a difference between sets, which we indicate by (–).
As sets A and B have the same color, we can say that there is a representation of the union of sets, that is, the joining of the elements of A and B, represented by A B.
Therefore, we can say that the hatched area is the difference of C from the union of A and B, that is, C – (A B).
question 7
In a pre-university course there are 600 students enrolled in isolated subjects. 300 students attend Mathematics, 200 students attend Portuguese classes and 150 students do not attend these subjects.
Considering the students enrolled in the course (U), students taking math (M) and students taking Portuguese (P), determine:
a) the number of Mathematics or Portuguese students
b) the number of Mathematics and Portuguese students
Right answer:
a) n (M P) = 450
b) n (M P) = 50
a) the number of students requested includes both Mathematics and Portuguese students. Therefore, we have to find the union of the two sets.
The result can be calculated by subtracting the total number of students in the school by the number of students not taking these subjects.
n (M P) = n (U) - 150 = 600 - 150 = 450
b) as the requested result is from students studying Mathematics and Portuguese, we have to find the intersection of the sets, that is, the elements common to both sets.
We can calculate the intersection of the two sets by adding the number of students enrolled in the subjects of Portuguese and Mathematics and then subtracting the number of students studying these two subjects at the same time.
n (M P) = n (M) + n (P) - n (M
P) = 300 + 200 - 450 = 50
question 8
Numerical sets include the following sets: Naturals (ℕ), Integers (ℤ), Rationals (ℚ), Irrationals (I), Reals (ℝ) and Complexes (ℂ). On the aforementioned sets, mark the definition that corresponds to each one of them.
1. natural numbers |
( ) covers all numbers that can be written as a fraction, with integer numerator and denominator. |
| 2. integers | ( ) corresponds to the union of rationals with irrationals. |
| 3. rational numbers | ( ) are decimal, infinite and non-periodic numbers and cannot be represented by irreducible fractions. |
| 4. irrational numbers | ( ) is formed by the numbers we use in the counts {0,1,2,3,4,5,6,7,8,...} |
| 5. real numbers | ( ) includes roots of type √-n. |
| 6. Complex numbers | ( ) gathers all the elements of natural numbers and their opposites. |
Correct answer: 3, 5, 4, 1, 6, 2.
(3) The rational numbers cover all numbers that can be written as a fraction, with integer numerator and denominator. This set includes non-exact divisions. ℚ = {x = a/b, with a ∈ ℤ, b ∈ ℤ and b ≠ 0}
(5) The real numbers correspond to the union of rationals with irrationals, that is, = ℚ ∪ I.
(4) The irrational numbers they are decimal, infinite, and non-periodic numbers and cannot be represented by irreducible fractions. The numbers in this group result from operations, the result of which could not be written as a fraction. For example to √ 2.
(1) The natural numbers are formed by the numbers we use in the counts ℕ = {0,1,2,3,4,5,6,7,8,...}.
(6) The complex numbers include roots of type √-n and so is an extension of real numbers.
(2) The whole numbers bring together all the elements of natural numbers and their opposites. To be able to solve all subtraction, such as 7 - 10, the set of naturals was extended, thus appearing the set of integers. ℤ= {..., -3,-2,-1,0,1,2,3,...}
question 9
(UNB-Adapted) From 200 people who were surveyed about their preferences in watching racing championships on television, the following data were collected:
- 55 of respondents do not watch;
- 101 watch Formula 1 races;
- 27 watch the Formula 1 and Motorbike races;
How many of the people interviewed watch, exclusively, Motorbike races?
a) 32
b) 44
c) 56
d) 28
Correct answer: b) 44.
Step 1: Determine the total number of people watching the races
For that, we just need to subtract the total number of respondents from those who declared not to attend the racing championships.
200 - 55 = 145 people
2nd step: calculate the number of people who watch only Motorbike races

74 + 27 + (x – 27) = 145
x + 74 = 145
x = 145 - 74
x = 71
Subtracting the value of x from the intersection of the two sets, we find the number of respondents who only watch motorcycle speed races.
71 - 27 = 44
question 10
(UEL-PR) At a given time, three TV channels had, in their programming, soap operas in their prime time: soap opera A on channel A, soap opera B on channel B and soap opera C on channel C. In a survey of 3000 people, it was asked which soap operas they liked. The table below indicates the number of viewers who designated the soap operas as enjoyable.
| Soap operas | Number of viewers |
| THE | 1450 |
| B | 1150 |
| Ç | 900 |
| A and B | 350 |
| A and C | 400 |
| B and C | 300 |
| A, B and C | 100 |
How many interviewed viewers do not find any of the three soap operas pleasant?
a) 300 viewers.
b) 370 viewers.
c) 450 viewers.
d) 470 viewers.
e) 500 viewers.
Correct answer: c) 450 viewers.
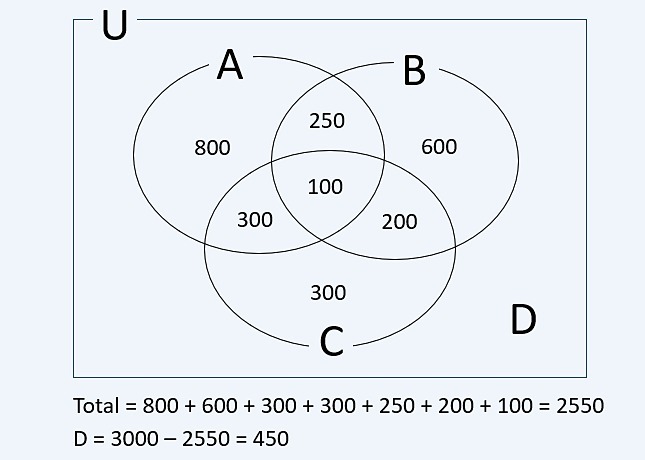
There are 450 viewers who do not find any of the three telenovelas pleasant.
Find out more by consulting the following texts:
- Set theory
- Operations with Sets
- Numerical sets
- Exercises on Numerical Sets
