We can consider the simple permutation as a particular case of arrangement, where the elements will form groupings that will differ only by order. The simple permutations of the P, Q, and R elements are: PQR, PRQ, QPR, QRP, RPQ, RQP. To determine the number of groupings of a simple permutation we use the following expression P = n!.
no!= n*(n-1)*(n-2)*(n-3)*...*3*2*1
For example
4! = 4*3*2*1 = 24
Example 1
How many anagrams can we form with the word CAT?
Resolution:
We can vary the letters in place and form several anagrams, formulating a case of simple permutation.
P = 4! = 24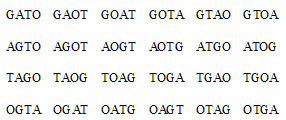
Example 2
How many different ways can we organize the models Ana, Carla, Maria, Paula and Silvia to produce a promotional photo album
Resolution:
Note that the principle to be used in the organization of the models will be simple permutation, as we will form groups that will only be differentiated by the order of the elements.
P = n!
P = 5!
P = 5*4*3*2*1
P = 120
Therefore, the number of possible positions is 120.
Example 3
How many different ways can we put six men and six women in a single file:
a) in any order
Resolution:
We can organize the 12 people differently, so we use
12! = 12*11*10*9*8*7*6*5*4*3*2*1 = 479,001,600 possibilities
b) starting with a man and ending with a woman
Resolution:
When we start the grouping with a man and end with a woman, we will have:
Six men randomly in first position.
Six women randomly in last position.
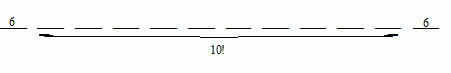
P = (6*6) * 10!
P = 36*10!
P = 130,636,800 possibilities
by Mark Noah
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/permutacao-simples.htm

