When studying the set of Rational Numbers, we find some fractions that, when converted to decimal numbers, become periodic decimals. To perform this transformation, we must divide the numerator of the fraction by its denominator, as in the case of the fraction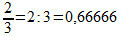 
. Likewise, through a periodic decimal, we can find the fraction that gave rise to it. This fraction is called “generating fraction”.
In any periodic decimal, the number that repeats is called the time course. In the example given, we have a simple periodic decimal, and the period is the number 6. Through a simple equation, we can find the generating fraction of 0,6666…
First, we can state that:
x = 0,666...
From there, we check how many digits the period has. In this case, the period has a digit. So let's multiply both sides of the equation by 10, if the period had 2 digits, we would multiply by 100, in the case of 3 digits, by 1000, and so on. So, we will have:
10x = 6,666...
In the second member of the equation, we can break the number 6,666... into a whole number and another decimal as follows:
10 x = 6 + 0,666...
However, right at the beginning we stated that x = 0.666..., so we can replace the decimal part of the equation with x and we're left with:
10 x = 6 + x
Using the basic properties of equations, we can then change the variable x from the second to the first side of the equation:
10 x - x = 6
Solving the equation, we will have:
9 x = 6
x = 6
9
Simplifying the fraction by 3, we have:
x = 2
3
Soon,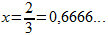 
, i.e, 
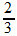is the generating fraction of the periodic decimal 0.6666... .
Let's see when we have a periodic composite decimal, as in the case of 0,03131… We'll start the same way:
x = 0,03131...
In order to make this equality more similar to the previous example, we need to change it so that we don't have any number between the equal sign and the period. For that, let's multiply the equation by 10:
10 x = 0,313131... ***
Following the reasoning used in the first example, we have that the periodic decimal has a two-digit period, so let's multiply the equation by 100.
1000 x = 31,313131...
Now it is enough to break the whole part of the decimal, in the second member of the equality.
1000 x = 31 + 0,313131...
but by ***, We have to 10 x = 0,313131..., let's replace the decimal number by 10 x.
1000 x = 31 + 10 x
1000 x - 10 x = 31
990 x = 31
x = 31
990
So the generating fraction of 0,0313131… é 31 . This rule can be applied to all periodic tithes.
990
By Amanda Gonçalves
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/geratriz-uma-dizima-periodica.htm
