The inverse matrix or invertible matrix is a type of square matrix, that is, it has the same number of rows (m) and columns (n).
It occurs when the product of two matrices results in a same-order identity matrix (same number of rows and columns).
Thus, to find the inverse of a matrix, multiplication is used.
THE. B = B. A = Ino (when matrix B is inverse of matrix A)
But what is the Identity Matrix?
THE Identity Matrix is defined when the elements of the main diagonal are all equal to 1 and the other elements are equal to 0 (zero). It is indicated by Ino:
Inverse Matrix Properties
- There is only one inverse for each matrix.
- Not all matrices have an inverse matrix. It is invertible only when the products of square matrices result in an identity matrix (Ino)
- The inverse matrix of an inverse corresponds to the matrix itself: A = (A-1)-1
- The matrix transposed of an inverse matrix is also inverse: (At) -1 = (A-1)t
- The inverse matrix of a transposed matrix corresponds to the transpose of the inverse: (A-1 THEt)-1
- The inverse matrix of an identity matrix is equal to the identity matrix: I-1 = I
See too: Matrices
Inverse Matrix Examples
2x2 Inverse Matrix
3x3 Inverse Matrix
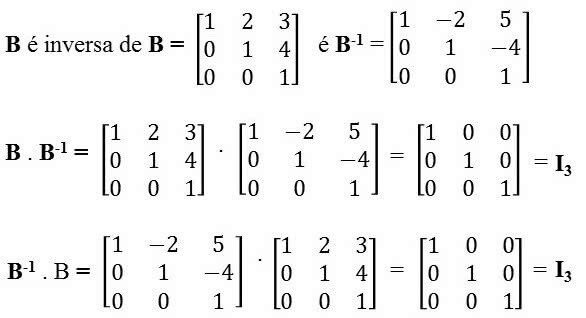
Step by Step: How to Calculate the Inverse Matrix?
We know that if the product of two matrices is equal to the identity matrix, this matrix has an inverse.
Note that if matrix A is the inverse of matrix B, the notation is used: A-1.
Example: Find the inverse of the matrix below 3x3 order.
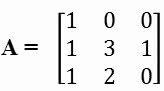
First of all, we must remember that A. THE-1 = I (The matrix multiplied by its inverse will result in the identity matrix Ino).
Each element of the first row of the first matrix is multiplied by each column of the second matrix.
Therefore, the elements of the second row of the first matrix are multiplied by the columns of the second.
And finally, the third row of the first with the columns of the second:
By matching the elements with the identity matrix, we can discover the values of:
a = 1
b = 0
c = 0
Knowing these values, we can calculate the other unknowns in the matrix. In the third row and first column of the first matrix we have a + 2d = 0. So let's start by finding the value of d, by replacing the values found:
1 + 2d = 0
2d = -1
d = -1/2
Likewise, in the third row and second column we can find the value of and:
b + 2e = 0
0 + 2e = 0
2e = 0
e = 0/2
e = 0
Continuing, we have in the third line of the third column: c + 2f. Note that the second identity matrix of this equation is not equal to zero, but equal to 1.
c + 2f = 1
0 + 2f = 1
2f = 1
f = ½
Moving to the second row and the first column we will find the value of g:
a + 3d + g = 0
1 + 3. (-1/2) + g = 0
1 - 3/2 + g = 0
g = -1 + 3/2
g = ½
In the second row and second column, we can find the value of H:
b + 3e + h = 1
0 + 3. 0 + h = 1
h = 1
Finally, let's find the value of i by the equation of the second row and third column:
c + 3f + i = 0
0 + 3 (1/2) + i = 0
3/2 + i = 0
i = 3/2
After discovering all the unknown values, we can find all the elements that make up the inverse matrix of A:
Entrance Exam Exercises with Feedback
1. (Cefet-MG) The matrix 
is inverse of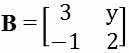 
It can be said, correctly, that the difference (x-y) is equal to:
a) -8
b) -2
c) 2
d) 6
e) 8
Alternative e: 8
2. (UF Viçosa-MG) Let the matrices be:
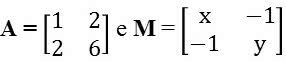
Where x and y are real numbers and M is the inverse matrix of A. So the xy product is:
a) 3/2
b) 2/3
c) 1/2
d) 3/4
e) 1/4
Alternative to: 3/2
3. (PUC-MG) The inverse matrix of the matrix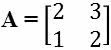 
it's the same as:
The)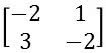 
B)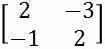 
ç) 
d) 
and) 
Alternative b: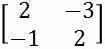
Read too:
- Matrices - Exercises
- Matrices and Determinants
- Types of Matrices
- Transposed Matrix
- Matrix Multiplication
