Test your knowledge with the proposed exercises and with questions that fell on the entrance exam about fractions and operations with fractions.
Be sure to check the commented resolutions to gain more knowledge.
Proposed exercises (with resolution)
Exercise 1
The trees in a park are arranged in such a way that if we build a line between the first tree (A) of a stretch and the last tree (B) we would be able to visualize that they are located at the same distance as one of the others.
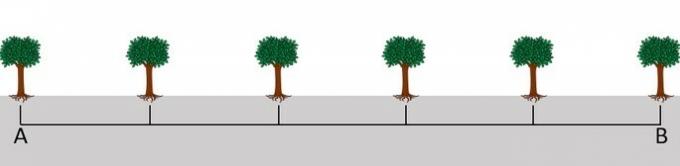
According to the image above, what fraction represents the distance between the first and second tree?
a) 1/6
b) 2/6
c) 1/5
d) 2/5
Correct answer: c) 1/5.
A fraction is a representation of something that has been divided into equal parts.
Notice that, from the image, the space between the first and last tree has been divided into five parts. So this is the denominator of the fraction.
The distance between the first and second tree is represented by only one of the parts and, therefore, it is the numerator.
Thus, the fraction that represents the space between the first and second tree is 1/5, because among the 5 sections in which the route was divided, the two trees are located in the first.
Exercise 2
Look at the candy bar below and answer: how many squares should you eat to consume 5/6 of the bar?

a) 15
b) 12
c) 14
d) 16
Correct answer: a) 15 squares.
If we count how many chocolate squares we have on the bar shown in the image, we will find the number 18.
The denominator of the fraction consumed (5/6) is 6, that is, the bar was divided into 6 equal parts, each with 3 small squares.

To consume the fraction of 5/6 then we must take 5 pieces of 3 squares each and thus consume 15 squares of chocolate.

Check out another way to resolve this issue.
As the bar has 18 squares of chocolate and you must consume 5/6, we can perform a multiplication and find the number of squares that corresponds to this fraction.
So, eat 15 squares to consume 5/6 of the bar.
Exercise 3
Mário filled 3/4 of a 500 mL jar with refreshment. When serving the drink, he distributed the liquid equally in 5 cups of 50 ml, occupying 2/4 of the capacity of each one. Based on these data, answer: what fraction of liquid is left in the jar?
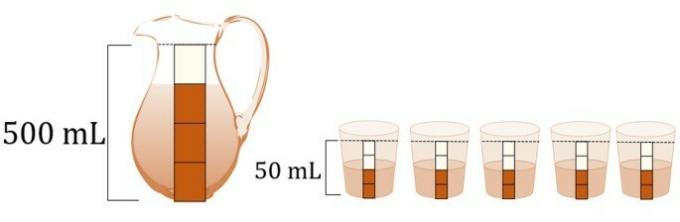
a) 1/4
b) 1/3
c) 1/5
d) 1/2
Correct answer: d) 1/2.
To answer this exercise we need to perform operations with fractions.
1st step: calculate the amount of soda in the jar.
2nd step: calculate the amount of refreshment in the glasses
As there are 5 glasses, so the total liquid in the glasses is:
3rd step: calculate the amount of liquid left in the jar
From the statement, the total capacity of the jar is 500 ml and by our calculations the amount of liquid left in the jar is 250 ml, that is, half its capacity. Therefore, we can say that the fraction of liquid that is left is 1/2 its capacity.
Check out another way to find the fraction.
As the jar was filled with 3/4 of the soft drink, Mário distributed 1/4 of the liquid into the glasses, leaving 2/4 in the jar, which is the same as 1/2.
Exercise 4
20 co-workers decided to place a bet and reward those who best hit the results of the games in a football championship.
Knowing that each person contributed 30 reais and that the prizes would be distributed as follows:
- 1st place: 1/2 of the amount collected;
- 2nd first place: 1/3 of the amount collected;
- 3rd place: Receives the remaining amount.
How much, respectively, did each winning participant receive?
a) BRL 350; BRL 150; BRL 100
b) BRL 300; BRL 200; BRL 100
c) BRL 400; BRL 150; BRL 50
d) BRL 250; BRL 200; BRL 150
Correct answer: b) BRL 300; BRL 200; BRL 100.
First, we must calculate the amount collected.
20 x BRL 30 = BRL 600
As each of the 20 people contributed R$30, then the amount used for the award was R$600.
To find out how much each winner received, we must divide the total amount by the corresponding fraction.
1st place:
2nd place:
3rd place:
For the last winner, we must add how much the other winners received and subtract from the amount collected.
300 + 200 = 500
600 - 500 = 100
Therefore, we have the following award:
- 1st place: R$300.00;
- 2nd place: R$ 200.00;
- 3rd place: R$ 100.00.
See too: Multiplication and Division of Fractions
Exercise 5
In a race car dispute, a competitor was 2/7 from finishing the race when he had an accident and had to abandon it. Knowing that the competition was held with 56 laps at the racecourse, which lap was the competitor removed from the track?
a) 16th lap
b) 40th lap
c) 32nd lap
d) 50th lap
Correct answer: b) 40th lap.
To determine which lap the competitor left the race we need to determine the lap that corresponds to 2/7 to finish the course. For this, we will use the multiplication of a fraction by an integer.
If there were 2/7 of the course left to finish the race, then there were 16 laps left for the competitor.
Subtracting the value found by the total number of returns we have:
56 – 16 = 40.
Therefore, after 40 laps the competitor was taken off the track.
Check out another way to resolve this issue.
If the competition is held with 56 laps at the racecourse and, according to the statement, there were 2/7 of the race to go, then the 56 laps correspond to the fraction 7/7.
Subtracting 2/7 from the total 7/7, we will find the route taken by the competitor to the place where the accident occurred.
Now, just multiply the 56 laps by the fraction above and find the lap that the competitor was taken off the track.
Thus, in both ways of calculating, we will find the result 40th lap.
See too: What is fraction?
Commented questions about entrance exams
question 6
ENEM (2021)
Antônio, Joaquim and José are partners in a company whose capital is divided, among the three, in proportional parts: 4, 6 and 6, respectively. With the intention of equaling the participation of the three partners in the company's capital, Antônio intends to acquire a fraction of the capital of each of the other two partners.
The fraction of the capital of each partner that Antônio must acquire is
a) 1/2
b) 1/3
c) 1/9
d) 2/3
e) 4/3
Answer: item c
From the statement we know that the company was divided into 16 parts, as 4 + 6 + 6 = 16.
These 16 parts must be divided into three equal parts for the members.
Since 16/3 is not an exact division, we can multiply by a common value without losing proportionality.
Let's multiply by 3 and check for equality.
4.3 + 6.3 + 6.3 = 16.3
12 + 18 + 18 = 48
48 = 48
Dividing 48 by 3 the result is exact.
48/3 = 16
Now, the company is divided into 48 parts, of which:
Antônio has 12 parts of the 48.
Joaquim has 18 parts out of 48.
José owns 18 parts of the 48.
Thus, Antônio, who is already 12, needs to receive another 4 to be left with 16.
For this reason, each of the other partners must pass 2 parts, out of 18, to Antônio.
The fraction that Antônio needs to acquire from a partner is 2/18, simplifying:
2/18 = 1/9
question 7
ENEM (2021)
A pedagogical game is formed by cards which have a fraction printed on one of their faces. Each player is dealt four cards and the one who first manages to increasingly sort their cards by their printed fractions wins. The winner was the student who received the cards with the fractions: 3/5, 1/4, 2/3 and 5/9.
The order that this student presented was
a) 1/4, 5/9, 3/5, 2/3
b) 1/4, 2/3, 3/5, 5/9
c) 2/3, 1/4, 3/5, 2/3
d) 5/9, 1/4, 3/5, 2/3
e) 2/3, 3/5, 1/4, 5/9
Answer: item a
To compare fractions they must have the same denominators. For this, we calculated the MMC between 5, 4, 3 and 9, which are the denominators of the fractions drawn.

To find the equivalent fractions, we divide 180 by the denominators of the fractions drawn and multiply the result by the numerators.
For 3/5
180 / 5 = 36, as 36 x 3 = 108, the equivalent fraction will be 108 / 180.
For 1/4
180/4 = 45, as 45 x 1 = 45, the equivalent fraction will be 45/180
for 2/3
180/3 = 60, as 60 x 2 = 120, the equivalent fraction will be 120/180
For 9/5
180/9 = 20, as 20 x 5 = 100. the equivalent fraction will be 100/180
With the equivalent fractions, just sort by the numerators in ascending order and associate with the drawn fractions.

question 8
(UFMG-2009) Paula bought two ice cream containers, both with the same amount of product.
One of the jars contained equal amounts of chocolate, cream, and strawberry flavors; and the other, equal amounts of chocolate and vanilla flavors.
So, it is CORRECT to state that, in this purchase, the fraction corresponding to the amount of chocolate flavored ice cream was:
a) 2/5
b) 3/5
c) 5/12
d) 5/6
Correct answer: c) 5/12.
The first pot contained 3 flavors in equal amounts: 1/3 chocolate, 1/3 vanilla and 1/3 strawberry.
In the second pot, there was 1/2 chocolate and 1/2 vanilla.
Schematically representing the situation, as shown in the image below, we have:
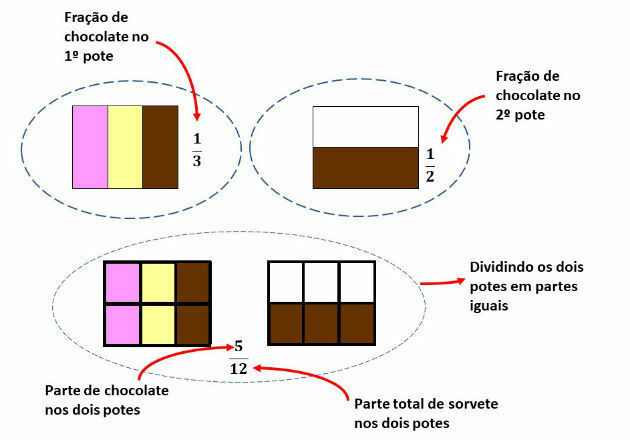
Note that we want to know the fraction corresponding to the amount of chocolate in the purchase, that is, considering the two ice cream jars, so we divide the two jars into equal parts.
In this way, each pot was divided into 6 equal parts. So in both pots we have 12 equal parts. Of these, 5 parts correspond to the chocolate flavor.
So, the answer correct is the letter C.
We could still solve this problem, considering that the amount of ice cream in each jar is equal to Q. So we have:
The denominator of the fraction sought will be equal to 2Q, as we have to consider that there are two pots. The numerator will equal the sum of the chocolate parts in each pot. Thus:
Remember that when we divide one fraction by another, we repeat the first, move to multiplication, and invert the second fraction.
See too: Fraction Simplification
question 9
(Unesp-1994) Two contractors will jointly pave a road, each working from one end. If one of them paves 2/5 of the road and the other the remaining 81 km, the length of that road is:
a) 125 km
b) 135 km
c) 142 km
d) 145 km
e) 160 km
Correct answer: b) 135 km.
We know that the total value of the road is 81 km (3/5) + 2/5. Through the rule of three we can find out the value in km of 2/5. Soon:
| 3/5 | 81 km |
| 2/5 | x |
We therefore find that 54 km is equivalent to 2/5 of the road. Now, just add this value to the other:
54 km + 81 km = 135 km
Therefore, if one of them paves 2/5 of the road and the other the remaining 81 km, the length of that road is 135 km.
If you are unsure about solving this exercise, please also read: Simple and Compound Three Rule.
question 10
(UECE-2009) A piece of fabric, after washing, lost 1/10 of its length and was measuring 36 meters. Under these conditions, the length, in meters, of the piece before washing was equal to:
a) 39.6 meters
b) 40 meters
c) 41.3 meters
d) 42 meters
e) 42.8 meters
Correct answer: b) 40 meters.
In this problem we need to find the value equivalent to 1/10 of the fabric that was shrunk after washing. Remember that 36 meters is therefore equivalent to 9/10.
If 9/10 is 36, how much is 1/10?
From the rule of three we can obtain this value:
| 9/10 | 36 meters |
| 1/10 | x |
We know then that 1/10 of the clothes are equivalent to 4 meters. Now, just add to the remaining 9/10:
36 meters (9/10) + 4 meters (1/10) = 40 meters
Therefore, the length, in meters, of the piece before washing was equal to 40 meters.
question 11
(ETEC/SP-2009) Traditionally, people from São Paulo usually eat pizza on weekends. João's family, consisting of him, his wife and their children, bought a giant size pizza cut into 20 equal pieces. It is known that John ate 3/12 and his wife ate 2/5 and there were N pieces left for their children. The value of N is?
a) 7
b) 8
c) 9
d) 10
e) 11
Correct answer: a) 7.
We know that fractions represent a part of a whole, which in this case is the 20 pieces of a giant pizza.
To solve this problem, we have to obtain the number of pieces corresponding to each fraction:
John: ate 12/3
John's wife: ate 2/5
N: what's left (?)
So let's find out how many pieces each of them ate:
John: 3/12 of 20 = 3/12. 20 = 60/12 = 5 pieces
Wife: 2/5 of 20 = 2/5. 20 = 8 pieces
If we add the two values (5 + 8 = 13) we have the amount of slices that were eaten by them. Therefore, there are 7 pieces left that were divided among the children.
question 12
(Enem-2011) The wetland is one of the most valuable natural heritages in Brazil. It is the largest continental wetland area on the planet - with approximately 210,000 km2, being 140 thousand km2 in Brazilian territory, covering part of the states of Mato Grosso and Mato Grosso do Sul. Heavy rains are common in this region. The balance of this ecosystem basically depends on the inflow and outflow of floods. The floods cover up to 2/3 of the Pantanal area. During the rainy season, the area flooded by floods can reach an approximate value of:
a) 91.3 thousand km2
b) 93.3 thousand km2
c) 140 thousand km2
d) 152.1 thousand km2
e) 233.3 thousand km2
Correct answer: c) 140 thousand km2.
First, we must note the values offered by the exercise:
210 thousand km2: total area
2/3 is the value that the floods cover in this area
To solve it, just know the value of the 2/3 of 210 thousand km2
210.000. 2/3 = 420 000/3 = 140 thousand km2
Therefore, during the rainy season, the area flooded by floods can reach an approximate value of 140,000 km2.
question 13
(Enem-2016) The tank of a certain passenger car holds up to 50 L of fuel, and the average efficiency of this car on the road is 15 km/L of fuel. When leaving for a trip of 600 km, the driver observed that the fuel marker was exactly on one of the marks on the marker's dividing scale, as shown in the following figure.

As the driver knows the route, he knows that there are, until arrival at his destination, five service stations. fuel supply, located 150 km, 187 km, 450 km, 500 km and 570 km from the point of match. What is the maximum distance, in kilometers, that you can travel until it is necessary to refuel the vehicle, so as not to run out of fuel on the road?
a) 570
b) 500
c) 450
d) 187
e) 150
b) 500.
To find out how many kilometers the car can travel, the first step is to find out how much fuel is in the tank.
For that, we have to read the marker. In this case, the pointer is marking half, plus half of half. We can represent this fraction by:
Therefore, 3/4 of the tank is full. Now, we have to know how many liters equals this fraction. As the fully filled tank is 50 liters, so let's find 3/4 of 50:
We also know that the car's efficiency is 15 km with 1 liter, so making a rule of three we find:
| 15 km | 1 liter |
| x | 37.5 km |
x = 15. 37,5
x = 562.5 km
Thus, the car will be able to travel 562.5 km with the fuel that is in the tank. However, it must stop before it runs out of fuel.
In this case, he will have to refuel after traveling 500 km, as it is the gas station before he runs out of fuel.
question 14
(Enem-2017) In a canteen, the summer sales success are juices made from fruit pulp. One of the best-selling juices is strawberry and acerola juice, which is prepared with 2/3 of strawberry pulp and 1/3 of acerola pulp.
For the merchant, the pulps are sold in packages of equal volume. Currently, strawberry pulp packaging costs R$ 18.00 and acerola pulp, R$ 14.70. However, a rise in the price of acerola pulp packaging is expected next month, starting to cost R$ 15.30.
In order not to increase the price of the juice, the merchant negotiated with the supplier a reduction in the price of the strawberry pulp packaging.
The reduction, in real, in the price of the strawberry pulp packaging should be of
a) 1.20
b) 0.90
c) 0.60
d) 0.40
e) 0.30
Correct answer: e) 0.30.
First, let's find out the cost of juice for the merchant, before the increase.
To find this value, let's add up the current cost of each fruit, taking into account the fraction used to make the juice. So we have:
So, this is the amount that will be kept by the merchant.
So, let's call it x the amount that the strawberry pulp must start to cost so that the total cost remains the same (R$16.90) and consider the new value of the acerola pulp:
As the question asks for a reduction in the price of strawberry pulp, then we still have to make the following subtraction:
18 - 17,7 = 0,3
Therefore, the reduction will have to be R$0.30.
question 15
(TJ EC). What fraction gives rise to the 2,54646 decimal… in decimal representation?
a) 2,521 / 990
b) 2,546 / 999
c) 2,546 / 990
d) 2,546 / 900
e) 2,521 / 999
Answer: item a
The part (period) that repeats is 46.
A common strategy for finding the generating fraction is to isolate the repeating part, in two ways.
Calling 2.54646… from x, we have:
X = 2.54646... (equation 1)
In equation 1, multiplying by 10 the two sides of the equality, we have:
10x = 25.4646... (equation 2)
In equation 1, multiplying by 1000 the two sides of the equality, we have:
100x = 2546.4646... (equation 2)
Now that in the two results, only 46 repeats, to eliminate it, let's subtract the second equation from the first.
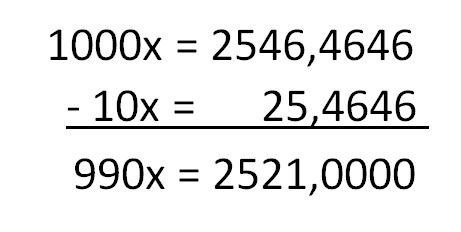
990x = 2521
Isolating x, we have:
x = 2521/990
Study more about this topic. Read too:
- Types of fractions and fractional operations
- Equivalent Fractions
- Addition and Subtraction of Fractions