The fundamental principle of counting, also called the multiplicative principle, is used to find the number of possibilities for an event consisting of n stages. For this, the steps must be successive and independent.
If the first stage of the event has x possibilities and the second stage consists of y possibilities, then there are x. and possibilities.
Therefore, the fundamental principle of counting is the multiplication of given options to determine total possibilities.
This concept is important for combinatorial analysis, an area of Mathematics that brings together methods for solving problems that involve counting and therefore it is very useful in investigating possibilities to determine the probability of phenomena.
Example 1
João is staying at a hotel and intends to visit the historic city center. From the hotel there are 3 subway lines that take you to the mall and 4 buses that travel from the mall to the historic center.

How many ways can João leave the hotel and get to the historic center through the mall?
Solution: The tree diagram or tree of possibilities is useful for analyzing the structure of a problem and visualizing the number of combinations.
Note how the verification of the combinations was done using the tree diagram.
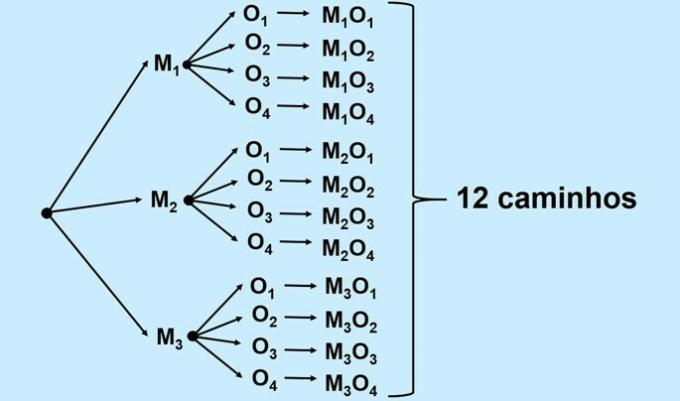
If there are 3 possibilities to leave the hotel and reach the mall, and from the mall to the historic center we have 4 possibilities, then the total number of possibilities is 12.
Another way to solve the example would be the fundamental principle of counting, making the multiplication of the possibilities, that is, 3 x 4 = 12.
Example 2
A restaurant has on its menu 2 types of starters, 3 types of main courses and 2 types of desserts. How many menus could be assembled for a meal with a starter, a main course and a dessert?
Solution: We will use the tree of possibilities to understand the set up of the menus with starter (E), main course (P) and dessert (S).
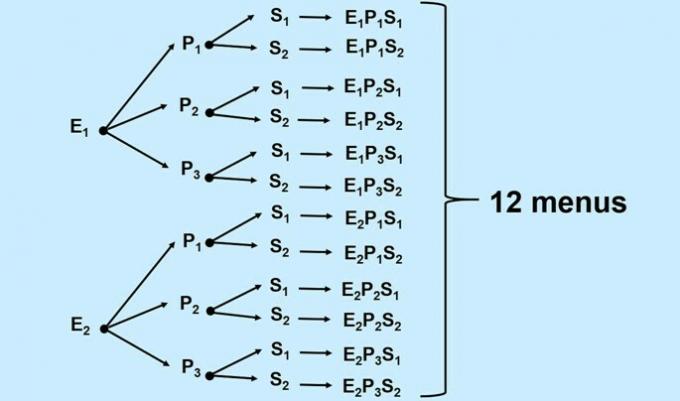
By the fundamental principle of counting, we have: 2 x 3 x 2 = 12. Therefore, 12 menus could be formed with a starter, a main course and a dessert.
solved exercises
question 1
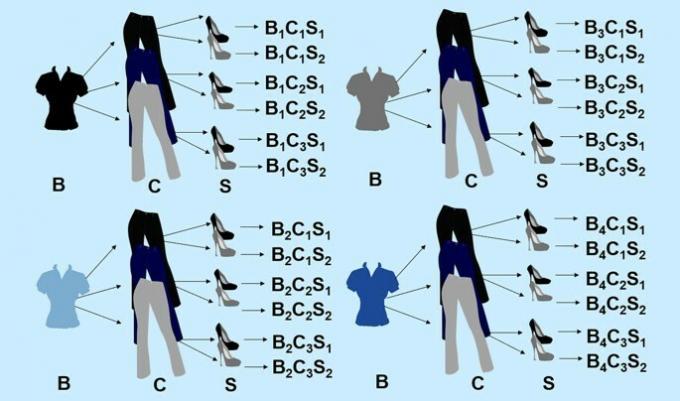
Ana was organizing to travel and packed 3 pants, 4 blouses and 2 shoes in her suitcase. How many combinations can Ana form with a pair of pants, a blouse and a shoe?
a) 12 combinations
b) 32 combinations
c) 24 combinations
d) 16 combinations
Correct alternative: c) 24 combinations.
Note that for each of the 4 blouses, Ana has 3 pants options and 2 shoes options.
So 4 x 3 x 2 = 24 possibilities.
Thus, Ana can form 24 combinations with the pieces of the suitcase. Check the results with the possibilities tree.
question 2
A teacher elaborated a test with 5 questions and the students had to answer it marking true (T) or false (F) for each one of the questions. How many different ways could the test be answered?
a) 25
b) 40
c) 24
d) 32
Correct alternative: d) 32 possible answers.
There are two distinct answer options in a sequence of five questions.
Using the fundamental principle of counting, we have:
2.2.2.2.2 = 32 possible answers for the test.
question 3
In how many ways can a 3-digit number be formed using 0, 1, 2, 3, 4 and 5?
a) 200
b) 150
c) 250
d) 100
Correct alternative: d) 100.
The number formed must contain 3 digits to fill the position of hundred, ten and one.
In the first position we cannot put the number 0, as it would be the same as having a number with 2 digits. So for the hundred we have 5 digit options (1, 2, 3, 4, 5).
For the second position, we cannot repeat the number that was used for hundred, but we can use zero, so in the ten we also have 5 digit options.
As we were given 6 digits (0, 1, 2, 3, 4 and 5) and two that were used previously cannot be repeated, so for the unit we have 4 digit options.
So 5 x 5 x 4 = 100. We have 100 ways to write a 3-digit number using 0, 1, 2, 3, 4 and 5.
Gain more knowledge with the following texts:
- Combinatorial Analysis
- Permutation
- Probability
- Combinatorial Analysis Exercises
- Probability Exercises



