THE triangle likeness is used to find the unknown measure of one triangle by knowing the measures of another triangle.
When two triangles are similar, the measurements of their corresponding sides are proportional. This relationship is used to solve many geometry problems.
So, take advantage of the exercises commented and solved to solve all your doubts.
Issues resolved
1) Sailor's Apprentice - 2017
See the figure below

A building casts a 30 m long shadow on the ground at the same instant that a six foot person casts a 2.0 m shadow. It can be said that the height of the building is worth
a) 27 m
b) 30 m
c) 33 m
d) 36 m
e) 40 m
We can consider that the building, its projected shadow and the sun's ray form a triangle. Likewise, we also have a triangle formed by the person, his shadow and the sun's ray.
Considering that the sun's rays are parallel and that the angle between the building and the ground and the person is the ground is equal to 90º, the triangles, indicated in the figure below, are similar (two angles equals).
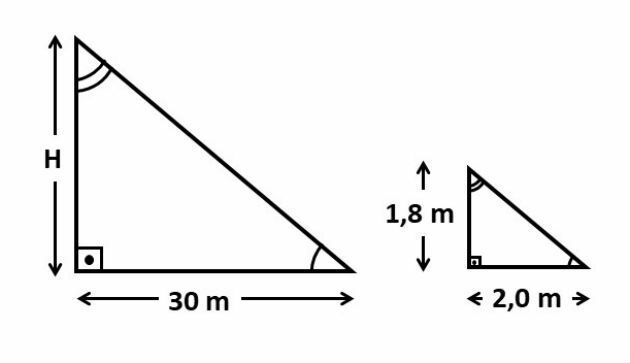
Since the triangles are similar, we can write the following proportion:
Alternative: a) 27 m
2) Fuvest - 2017
In the figure, rectangle ABCD has sides of length AB = 4 and BC = 2. Let M be the midpoint of the side and N the midpoint of the side
. The segments
intercept the segment
at points E and F, respectively.
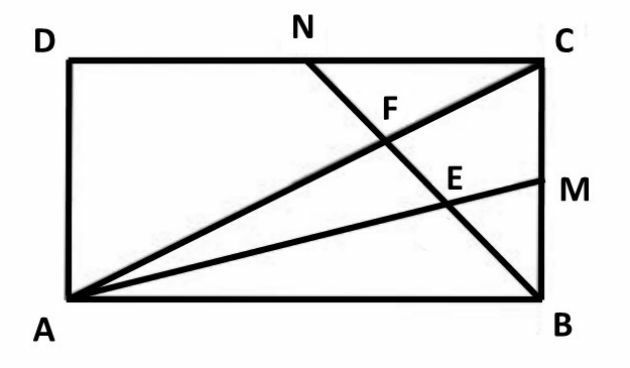
The area of triangle AEF is equal to
The area of triangle AEF can be found by decreasing the area of triangle ABE from the area of triangle AFB, as shown below:
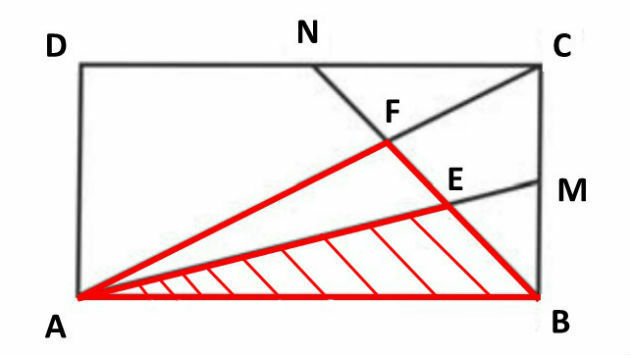
Let's start by finding the area of the AFB triangle. For this, we need to find out the height value of this triangle, as the base value is known (AB = 4).
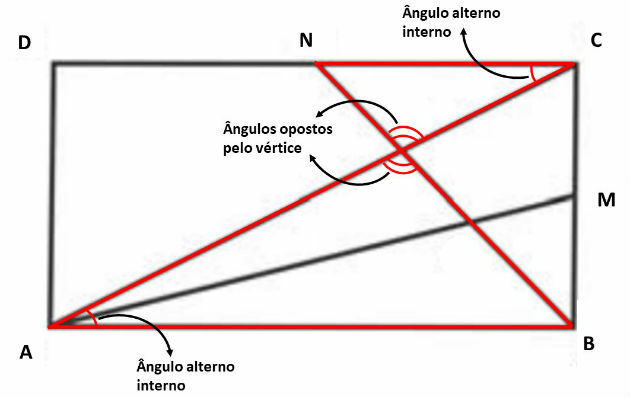
Note that triangles AFB and CFN are similar in that they have two equal angles (case AA), as shown in the figure below:
Let's plot the height H1, relative to side AB, in triangle AFB. As the measure of side CB is equal to 2, we can consider that the relative height of side NC in triangle FNC is equal to 2 - H1.

We can then write the following proportion:
Knowing the height of the triangle, we can calculate its area:
To find the area of triangle ABE, you will also need to calculate its height value. For this, we will use the fact that the ABM and AOE triangles, indicated in the figure below, are similar.

In addition, triangle OEB is a right triangle and the other two angles are equal (45º), so it is an isosceles triangle. Thus, the two legs of this triangle are worth H2, as the image below:
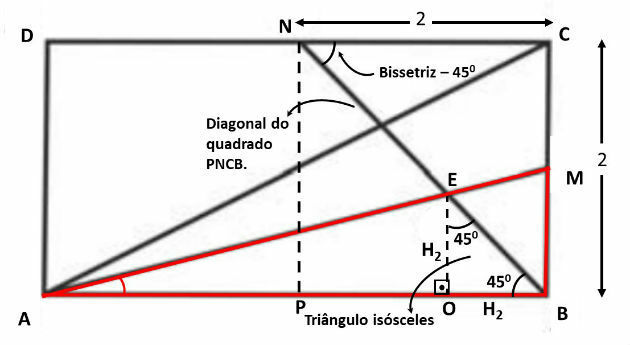
Thus, the side AO of triangle AOE is equal to 4 - H2. Based on this information, we can indicate the following proportion:
Knowing the height value, we can now calculate the area of triangle ABE:
Thus, the area of the triangle AFE will be equal to:
Alternative: d)
3) Cefet/MG - 2015
The following illustration represents a rectangular pool table, with a width and length equal to 1.5 and 2.0 m, respectively. A player must throw the white ball from point B and hit the black ball at point P, without hitting any of the other ones, first. As the yellow one is at point A, this player will throw the white ball to point L, so that it can bounce and collide with the black one.
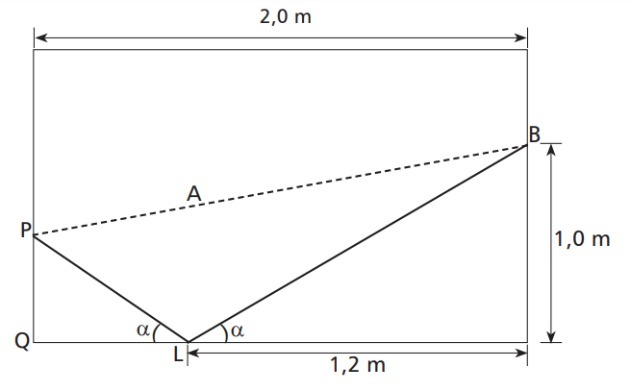
If the angle of the ball's incidence path on the side of the table and the bouncing angle are equal, as shown in the figure, then the distance from P to Q, in cm, is approximately
a) 67
b) 70
c) 74
d) 81
The triangles, marked in red in the image below, are similar, as they have two equal angles (angle equal to α and angle equal to 90º).

Therefore, we can write the following proportion:
Alternative: a) 67
4) Military College/RJ - 2015
In a triangle ABC, points D and E belong respectively to sides AB and AC and are such that DE / / BC. If F is a point of AB such that EF / / CD and the measurements of AF and FD e are, respectively, 4 and 6, the measurement of the segment DB is:
a) 15.
b) 10.
c) 20.
d) 16.
e) 36.
We can represent the triangle ABC, as shown below:
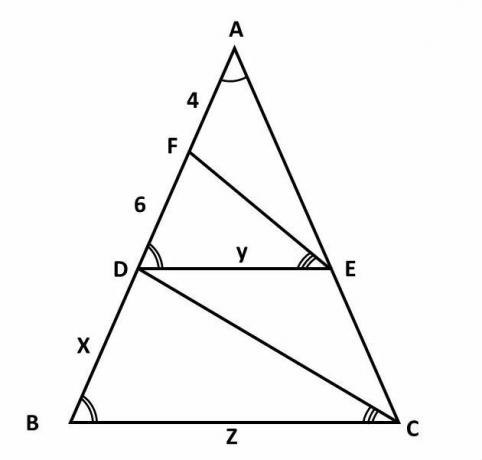
Since the segment DE is parallel to BC, then the triangles ADE and ABC are similar in that their angles are congruent.
We can then write the following proportion:
Triangles FED and DBC are also similar, as segments FE and DC are parallel. Thus, the following proportion is also true:
Isolating the y in this proportion, we have:
Replacing the y value in the first equality:
Alternative: a) 15
5) Epcar - 2016
A land in the shape of a right triangle will be divided into two lots by a fence made on the bisector of the hypotenuse, as shown in the figure.
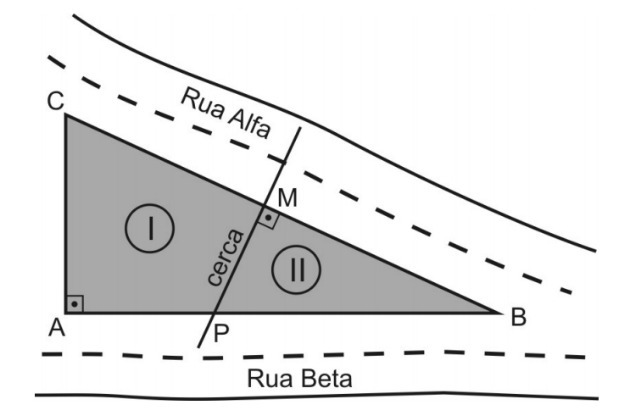
It is known that the sides AB and BC of this terrain measure, respectively, 80 m and 100 m. Thus, the ratio between the perimeter of lot I and the perimeter of lot II, in that order, is
To find out the ratio between the perimeters, we need to know the value of all sides of figure I and figure II.
Note that the bisector of the hypotenuse divides the BC side into two congruent segments, so the CM and MB segments measure 50 m.
Since the triangle ABC is a rectangle, we can calculate the side AC, using the Pythagorean theorem. However, note that this triangle is a Pythagorean triangle.
Thus, the hypotenuse being equal to 100 (5. 20) and one two legs equal to 80 (4.20), then the other leg can only be equal to 60 (3.20).
We also identified that triangles ABC and MBP are similar (case AA), as they have a common angle and the other equal to 90º.
So, to find the value of x we can write the following proportion:
The value of z can be found considering the proportion:
We can also find the value of y by doing:
Now that we know all sides, we can calculate the perimeters.
Perimeter of Figure I:
Perimeter of Figure II:
Therefore, the ratio between the perimeters will be equal to:
Alternative: d)
6) Enem - 2013
The owner of a farm wants to put a support rod to better secure two posts with lengths equal to 6 m and 4 m. The figure represents the real situation in which the posts are described by the segments AC and BD and the rod is represented by the EF segment, all perpendicular to the ground, which is indicated by the straight line segment AB. Segments AD and BC represent steel cables that will be installed.
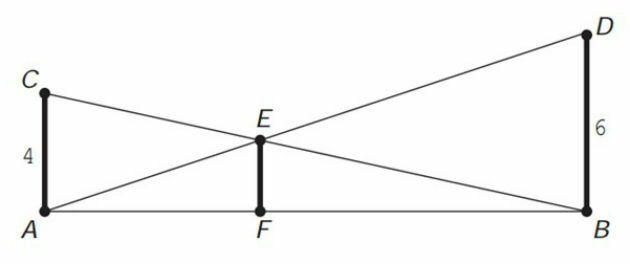
What should be the value of the rod length EF?
a) 1 m
b) 2 m
c) 2.4 m
d) 3 m
e) 2 m
To solve the problem, let's call the stem height as z and the measurements of the AF and FB segments of x and y, respectively, as shown below:
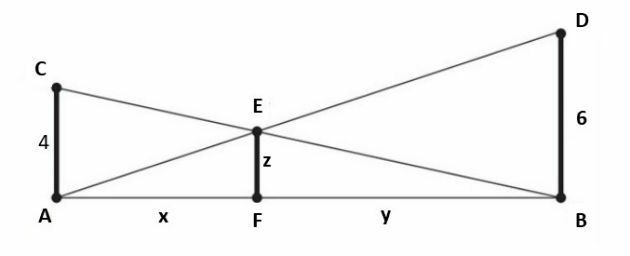
Triangle ADB is similar to triangle AEF in that both have an angle equal to 90° and a common angle, so they are similar in the case AA.
Therefore, we can write the following proportion:
Multiplying "in a cross", we get equality:
6x = h (x + y) (I)
On the other hand, the triangles ACB and FEB will also be similar, for the same reasons presented above. So we have the proportion:
Solving in the same way:
4y = h (x + y) (II)
Note that equations (I) and (II) have the same expression after the equal sign, so we can say that:
6x = 4y
Substituting the value of x in the second equation:
Alternative: c) 2.4 m
7) Fuvest - 2010
In the figure, triangle ABC is rectangular with sides BC = 3 and AB = 4. In addition, point D belongs to the collarbone. , the point E belonging to the collarbone
and point F belongs to the hypotenuse
, such that DECF is a parallelogram. if
, so the area of the DECF parallelogram is worth
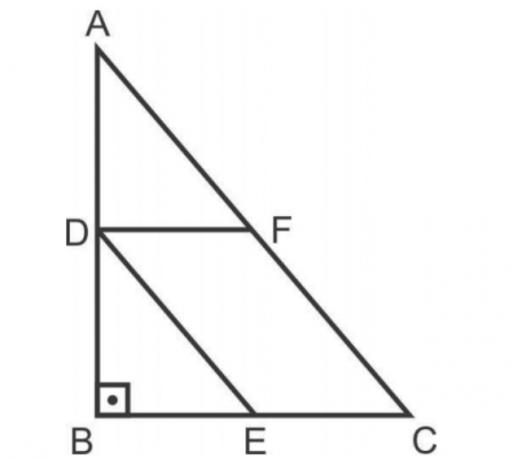
The parallelogram area is found by multiplying the base value by the height. Let's call h the height and x the base measure, as shown below:
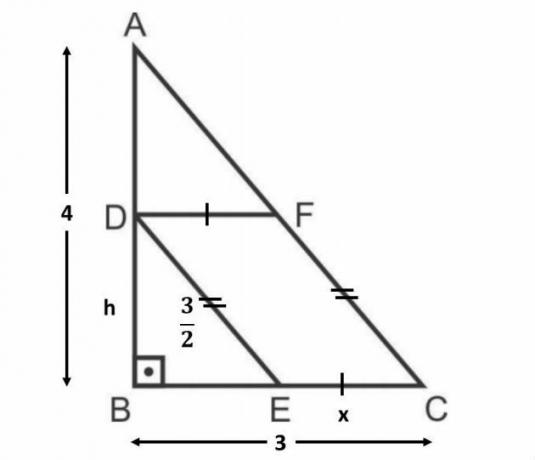
Since DECF is a parallelogram, its sides are parallel two by two. In this way, sides AC and DE are parallel. So the angles they are the same.
We can then identify that triangles ABC and DBE are similar (case AA). We also have that the hypotenuse of triangle ABC is equal to 5 (triangle 3,4 and 5).
In this way, let's write the following proportion:
To find the measure x of the base, we will consider the following proportion:
Calculating the parallelogram area, we have:
Alternative: a)

