fractions are representations for the division between whole numbers. The number at the top has the same role as the dividend and is called numerator. What is at the bottom plays the role of a divider and is called denominator.
Every fraction belongs to the set of rational numbers, in which all basic mathematical operations and their results are defined. Therefore, potentiation and rooting are well-defined operations on fractions and can be carried out easily if the correct property is used.
→ Potentiation of fractions: a result of multiplication
THE multiplication of fractions should be done as follows: the numerator of the result is the product of the denominators of the fractions, and the denominator of the result is the product of the numerators of the fractions. Look at an example where fractions are equal:

Note that since fractions are equal, then they are the basis of the following power:

In this way, we can define the potentiation of fractions in the following way:

Thus, if it is necessary to calculate a power involving a fraction, it is enough to raise the numerator and denominator separately to that exponent.
→ Fraction Radiation
As rooting is the inverse process of potentiation, we can define the nth root (nth: indeterminate number of times) of a fraction as follows:

This means that to calculate the root of a fraction, it is enough to calculate the root of the denominator and the numerator separately.
Examples
1) Note how the root resolution below is done. Simply calculate the denominator and numerator roots separately, as this is how the multiplication process is done.
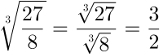
2) Check the resolution of a power of fractions, where the denominator and numerator are raised to the fourth power separately.
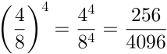
By Luiz Paulo Moreira
Graduated in Mathematics


