There are some properties basics about proportionality when a bundle of parallel lines is cut by a transverse straight. Before talking about these rules, it is important to be clear about these concepts. Are we going to understand them better?
Bundle of parallel and transverse lines
parallel lines and cross straights are concepts obtained from relative position between straight lines in the plane. We say that two lines are parallel when, in all their infinite extension, there is no meeting point between them.
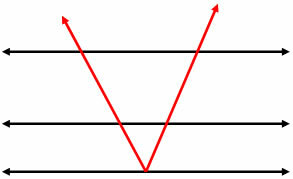
It is entirely possible that there are more than two parallel lines on the same plane. In fact, there are endless of them. Suppose there are three lines: r, s and t. Suppose r is parallel to line s and s is parallel to line t. Therefore, we can conclude that r is also parallel to the line t and that we have a bundle of parallel lines formed by three lines.

Lines r, s and t parallel to each other
Therefore, a bundle of parallel lines is a set of parallel lines.
cross straight is the one that cuts a bundle of parallel lines. If a line v cuts a line r from a beam of parallel lines, then it will cut all the straight lines in that beam.
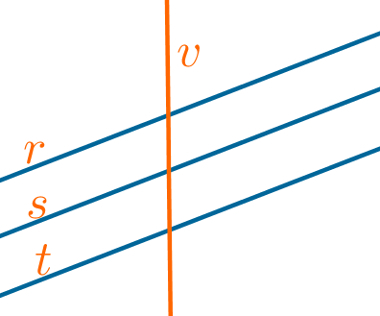
Straights of a beam being cut by a transverse
Properties of a bundle of parallel lines
in any straight bundle parallel cut by a cross, the following properties can be observed:
You corresponding angles are congruent. The corresponding angles between parallel and a transverse straight line are shown with the same letters in the following figure:

If one beam in parallel lines divide a line cross in straight segments congruent, will divide any other transverse line by the same proportion. In the following image, for example, the line r is cut into congruent segments. Note that the measurements of the segments on the line v are also congruent.
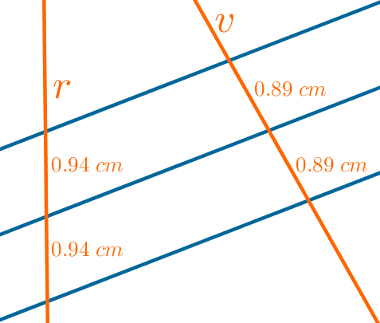
If one beam in parallel lines divide a line cross in proportional line segments, it will split any other transversal line in the same proportion, that is, a bundle of parallel lines divides two transversal lines into proportional segments.
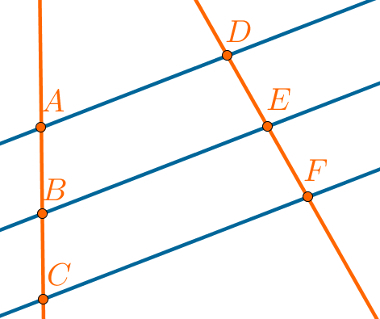
In this image, the segments are in the following proportion:
AB = IN
BC EF
The property above is known as Thales' Theorem.
Take the opportunity to check out our video lesson on the subject: