Sum and Product in 2nd Degree Equations

Sum and Product is a method applied in 2nd degree equations with the aim of finding their respective roots.

The method of sum and product is often used as an alternative to Bhaskara's Formula, as it consists of a simpler and quicker technique to obtain the intended results.

However, applying the sum and product in a 2nd degree equation is advised only when its coefficients are whole numbers. If they are fractioned, for example, Bhaskara's scheme may be easier.

How to use the sum and product method

To use this technique, you need to apply two different formulas:

sum of roots

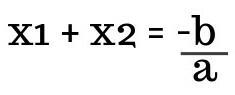
Root product

To find coefficient values The, B and ç, it is necessary to observe the 2nd degree equation: ax² + bx + c = 0.

The values ​​obtained in x1 and x2 must correspond with the respective result of addition and multiplication in both formulas.

Example:

In a 2nd degree equation: x² - 7x + 10 = 0

sum of roots

x1 + x2 = -(-7)/1
x1 + x2 = 7

Root product

x1 * x2 = 10/1
x1 * x2 = 10

Now, from the logical deduction, we need to find two numbers that add up to 7 and that multiplied result in 10.

Thus, the hypotheses of numbers that result in product 10 are:

1 * 10 = 10 or 2 * 5 = 10

To find out what the correct roots are, we need to check the sum. Among the available options it is proven that 2 and 5 are the correct results, since 2 + 5 = 7.

In this way, it turns out that the roots of the initial equation are x' = 2 and x'' = 5.

When should the sum and product method be applied?

Not all 2nd degree equations will allow the use of sum and product. If it is not possible to find two numbers that satisfy both the sum and the formulas of the multiplication, then it is necessary to use another method of solving, such as Bhaskara's echema, by example.

Example:

High School Equation: x²+ 3x + 5 = 0

Sum of roots: x1 + x2 = -3/1 = -3
Root product: x1 * x2 = 5/1 = 5

In this case, the roots to match the product should be 5 and 1. However, the sum of these two digits is different from -3. Thus, it becomes impossible to determine the roots of the equation through the method of sum and product.