At trigonometric relations are formulas that relate the angles and sides of a right triangle. These formulas involve the functions sine, cosine and tangentand have many applications in geometric problems involving this type of triangle.
Trigonometric relations in the right triangle
O right triangle it is the triangle that has a right angle (90°) and two acute angles (less than 90°). The sides of the right triangle are called the hypotenuse and sides, and the sides can be opposite or adjacent, depending on the reference angle.
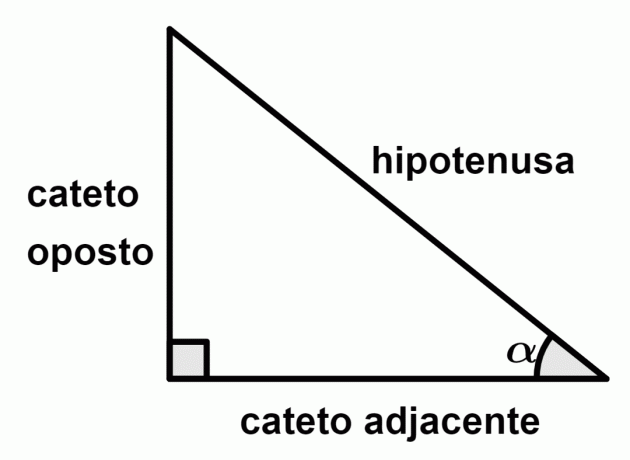
Elements of the right triangle:
- Hypotenuse: side opposite right angle;
- Opposite side: side opposite the considered acute angle;
- Adjacent side: side consecutive to the considered acute angle.
Formulas:
considering the angle of the right triangle, we have to:
Note: The hypotenuse of the right triangle is always the same, the opposite and adjacent sides vary in relation to the acute angle under consideration.
Examples - Using Trigonometric Relationships
Below are examples of how to use trigonometric relationships.
Example 1: Calculate the value of x and y in the triangle below:
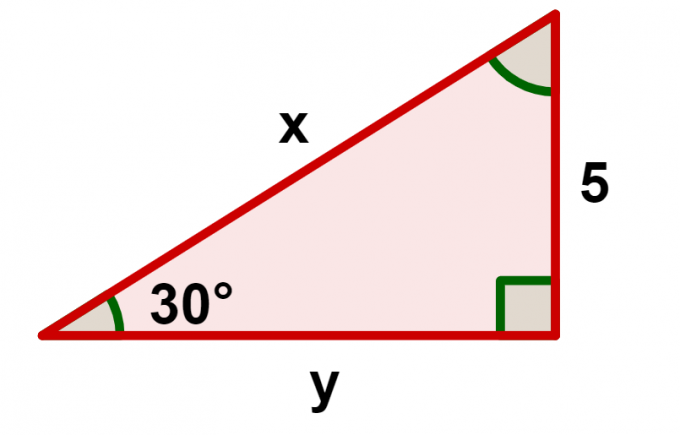
From the sine of the 30° angle, we can determine the value of x, which is the hypotenuse of the triangle.
- Free Online Inclusive Education Course
- Free Online Toy Library and Learning Course
- Free Online Math Games Course in Early Childhood Education
- Free Online Pedagogical Cultural Workshops Course
Now, one of the ways to find the value of y is from the cosine of the 30° angle. In this case, y is the leg adjacent to the 30° angle.
Example 2: Determine the measure of the angles and
from the triangle below:
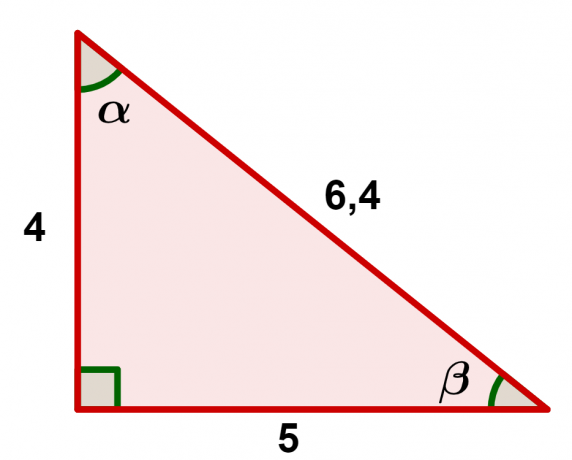
First, let's determine the angle :
Now let's determine the angle :
Note that we used sine in both cases, but we could also use cosine and arrive at these same results.
You may also be interested:
- trigonometric table
- trigonometric circle
- Derived relationships
- List of Trigonometry Exercises
- Sine and Cosine of Obtuse Angles
The password has been sent to your email.

