Exercises on similarity of triangles

similar triangles they are triangles that have the three corresponding angles with the same measure and the sides proportional.

The division of measurements from the proportional sides is a constant value, called the proportionality ratio.

There are some specific cases to identify similar triangles:

Case 1) Angle - Angle (AA)

Two triangles that have two corresponding angles of the same measure are similar.

Case 2) Side - Side - Side (LLL)

Two triangles that have the three sides proportional are similar.

Case 3) Side - Angle - Side (LAL)

Two triangles that have two proportional sides and an angle of the same measure between them are similar.

Also, we must remember the fundamental theorem of similarity between triangles:

If we draw a line that intersects two sides of a triangle at different points and that is parallel to the third side of the triangle, we get another triangle that is similar to the first.

To learn more about this subject, check out a list of exercises on similarity of triangles.

Index

instagram story viewer

List of Triangle Similar Exercises
Resolution of question 1
Resolution of question 2
Resolution of question 3
Resolution of question 4
Resolution of question 5
Resolution of question 6

List of Triangle Similar Exercises

Question 1. Determine the value of segment AB in the figure below:

Question 2. Determine the value of x in the figure below:

Question 3. Check if the triangles below are similar:

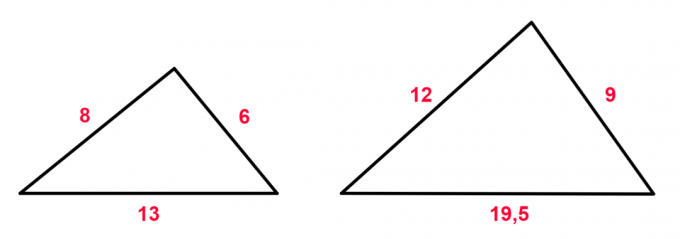
Question 4. Determine if the triangles below are similar:

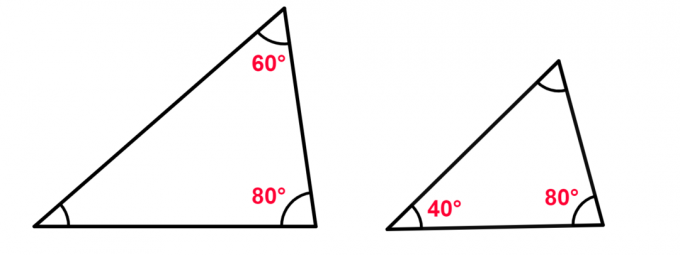
Question 5. Check if the triangles below are similar:

Question 6. Knowing that the segments $\inline \large \bg_white \overline{RS}$ and $\overline{AC}$ are parallel, determine the measure of $\inline \large \bg_white \overline{RS}$ .

Resolution of question 1

Since triangles ABC and OPQ have two corresponding angles of the same measure, then the triangles are similar.

Due to the similarity between the triangles, we have that:

$\frac{9}{\overline{AB}} =\frac{15}{5}$

$\Rightarrow \overline{AB} = 3$

Resolution of question 2

Triangles have two corresponding angles of the same measure, so they are similar.

Due to the similarity between the triangles, we have that:

$\mathrm{\frac{x}{3} = \frac{48}{x}}$

Check out some free courses

Free Online Inclusive Education Course
Free Online Children's Learning and Toy Library Course
Free Online Math Games Course in Early Childhood Education
Free Online Pedagogical Cultural Workshops Course

$\Rightarrow \mathrm{x}^2 = 144$

$\Rightarrow \mathrm{x} = 12$

Resolution of question 3

Let's check if the sides of triangles are proportional:

Side 1:

$\frac{8}{12} = \frac{2}{3}$

Side 2:

$\bg_white \frac{6}{9} = \frac{2}{3}$

Side 3:

$\frac{13}{19.5} = \frac{2}{3}$

So the triangles are similar and the ratio is 2/3.

Resolution of question 4

We must remember that the sum of the interior angles of a triangle is equal to 180°. In this way, we can find out the value of the unknown angle in each triangle.

Major triangle:

180° – 80° – 60° = 40°

→ The three angles of this triangle are: 80°, 60° and 40°.

Minor triangle:

180° – 80° – 40° = 60°

→ The three angles of this triangle are: 80°, 40° and 60°.

So the two triangles have two corresponding angles of the same measure, so they are similar.