Calculation of slope

O slope of a line is a value that indicates the slope of the line in relation to the abscissa axis (x axis).

There are a few different ways to calculate the slope, let's see what they are?

Calculation of slope

Consider, for example, the line in the figure below:

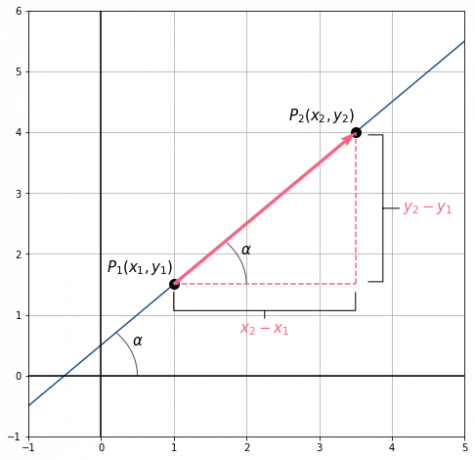
The slope corresponds to tangent of the angle $\dpi{120} \alpha$ . Thus, representing the slope by the letter $\dpi{120} m$ , We have to:

$\dpi{120} m = tan\: (\alpha)$

And we can establish some different ways to calculate the slope.

Calculating the slope from the angle

Knowing the angle of inclination, just calculate the tangent of that angle.

Example: if $\dpi{120} \alpha = 45^{\circ}$ , then:

$\dpi{120} m = tan\: (\alpha)$

$\dpi{120} m = tan\: (45^{\circ})$

$\dpi{120} m = 1$

To know the value of the tangent of an angle, just consult a trigonometric table.

Calculation of slope from two points

Check out some free courses

Free Online Inclusive Education Course
Free Online Toy Library and Learning Course
Free Online Math Games Course in Early Childhood Education
Free Online Pedagogical Cultural Workshops Course

If we know two points that belong to the line, $\dpi{120} \mathrm{P(x_1,y_1)}$ and $\dpi{120} \mathrm{P(x_2,y_2)}$ , we can calculate the slope as follows:

$\dpi{120} m = \frac{\mathrm{y_2 - y_1}}{\mathrm{x_2-x_1}}$

To understand this formula, notice that in the figure, a right triangle, with $\dpi{120} sin \, (\alpha) =\mathrm{ y_2 - y_1}$ and $\dpi{120} cos \, (\alpha) =\mathrm{ x_2 - x_1}$ and remember that $\dpi{120} tan(\alpha) = \frac{sen(\alpha)}{cos(\alpha)}$ .