Geometric shapes: what they are, examples, exercises

The study of geometric shapes developed several important concepts, such as the polygon study, flat figures enclosed by polygonals, and also of the polyhedra, spatial geometric solids that have faces formed by polygons.

In addition to these geometric shapes, there are, in plane geometry, those that are not polygons, such as the circumference, and, in spatial geometry, there are non-polyhedra, such as round bodies, among other solids. In addition to these geometric shapes, there are fractals, geometric figures created with a pattern: by increasing the scale, the parts of the figure will always be equal to the figure itself, having infinite mathematical patterns in its composition.

Read too: What is the difference between flat figures and spatial figures?

Geometry studies these shapes to explain the shapes of nature and the environment in which we live.

What are flat shapes?

Much of the geometry, known as plane geometry, is developed in a two-dimensional universe. We have as flat shapes any figures that have two dimensions,

like a square, a circle or even the representation of a two-dimensional star, as we are used to seeing. In flat shapes, there is a classification between polygons and non-polygons.

Do not stop now... There's more after the advertising ;)

• Polygons

For a flat shape to be considered a polygon, she needs to meet some criteria. The definition of a polygon is that it is a flat figure closed by straight segments. In a polygon, these straight lines can't cross.

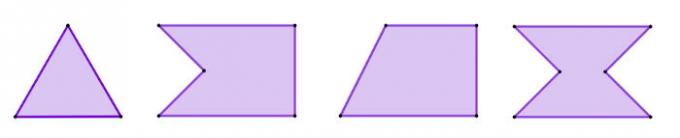
Some polygons are widely studied, developing formulas for calculating area and perimeter, in addition to studying their properties. The main polygons are:

• triangle
• quadrilateral
• Pentagon
• hexagon

• not polygons

Not all flat figures can be classified as polygons, so we know them as non-polygons. In order not to be a polygon, it is enough not to satisfy one of the characteristics of its definition, for example: if the flat figure has curves or if the segments intersect or if the figure is not closed, it will not be a polygon. Çícircles and circular sectors are examples of non-polygons that are very present in our reality.

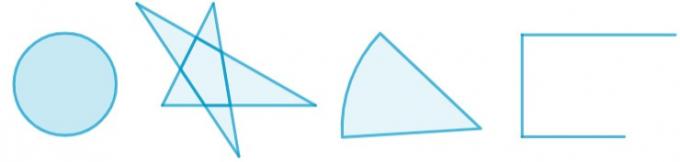
Figures such as the circumference and the circular sector are as studied as polygons, with the study of their elements and their properties. On the other hand, unclosed figures or whose segments intersect are less present in studies of plane geometry.

See too: How to plan geometric solids?

What are non-planar shapes?

When we are working with the third dimension, these figures are no longer flat and become geometric solids because they have three dimensions. Present in everyday life, solids are divided into two large groups, polyhedra and non-polyhedra. This geometry is known as spatial geometry, for working with three-dimensional space.

• Polyhedra

For a geometric solid to be considered a polyhedron, it must have faces formed by polygonal. The study of these solids is also quite frequent. The main polyhedra are the pyramids and prisms, and there are also the Plato's solids, for example.

Polyhedra are geometric solids whose faces are polygons.

The properties and formulas of each case of polyhedron they are also extensively studied, and it is common to calculate the volume and the total area.

• No polyhedra

Non-polyhedrons are solids that do not meet the definition of polyhedron, that is, do not have all faces formed by polygons, so the solids of revolution or round bodies. It is quite common, in sports practice, for the ball to have a spherical shape, in this case, we are dealing with a non-polyhedron. Besides the ball, we know the cylinders it's the cone.

Round bodies are examples of non-polyhedra.

fractals

Fractals are geometric figures with a very high complexity, being research objects of several mathematicians today. What is fascinating about fractal geometry is that each part is similar to its whole. There is a pattern throughout the figure that is repeated in each of its parts, which you can see using smaller scales. This pattern is quite common in nature, such as in snowflakes and vegetables.

Fractals are quite common in nature.

The study of fractals is more complex than we think, and many mathematicians are dedicated to this geometry, known as fractal geometry. With the help of computation, this area of ​​mathematics searches for equations that model the behavior of a fractal.

Also access: How to find the center of a circle?

solved exercises

Question 1 - About polygons, classify the following statements as true or false:

I – Every figure enclosed in the plane is a polygon.

II – Polygons have two dimensions.

III – Figures such as a circle make up the group of non-polygons.

We can say that:

A) Only I is false.

B) Only II is false.

C) Only III is false.

D) All are false.

E) All are true.

Resolution

Alternative A.

I – False → to be a polygon, the figure is not enough to be closed, it needs to be closed by polygonals, that is, by straight lines. Figures like the circle are closed, yet they are not polygons.

II → True → polygons are plane geometry objects that have two dimensions.

III → True → the circle is a non-polygon.

Question 2 - American football is a sport traditionally played in the United States. Your ball has a different shape than a conventional soccer ball, which is spherical. About the shape of the American football, we can say:

A) It is a figure of plane geometry classified as a polygon.

B) It is a figure of plane geometry classified as non-polygon.

C) She is a figure of spatial geometry classified as a polyhedron.

D) She is a figure of spatial geometry classified as non-polyhedron

Resolution

Alternative D. The American football ball has three dimensions, so it is the object of study of spatial geometry, in addition, it has a rounded shape, although it is not spherical. Still, it is possible to see that it does not have faces formed by polygons, which makes it a non-polyhedron.

By Raul Rodrigues de Oliveira
Maths teacher