Logarithm is a very important tool not only for the area of math, as it has application in several fields of science, such as geography, chemistry and computing.
Historically the logarithm arises in order to facilitate accounts that appeared frequently in several scientific areas. John Napier pioneered the study of logarithms, and managed to develop the operation capable of transforming products in sum, divisions into subtractions and potencies in multiplications.
Defining this operation, over time, other mathematicians formalized definitions and properties, in addition, the well-known log table.
Definition of the logarithm
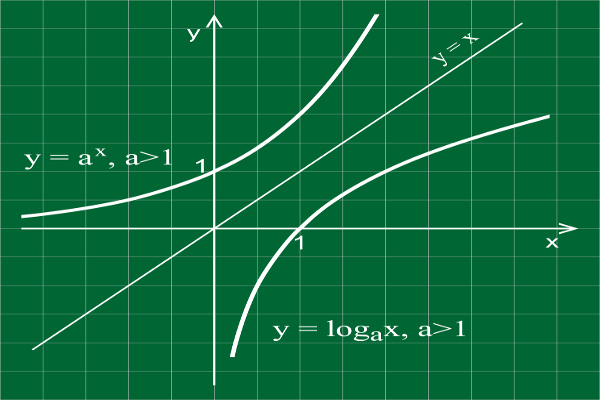
Sketch the graph of the logarithm function (right) and its exponential inverse (left).
consider two real numbers positive The and B, with to ≠ 0. the logarithm of B at the base The is the number x if, and only if, The raised to x is equal to the number B.
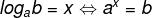
Nomenclature:
the → base
b → logarithm
x → logarithm
See the examples:
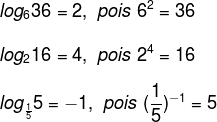
When a logarithm has a base equal to 10, it is called
decimal logarithm. When registering a decimal log, it is not necessary to write base 10. It is agreed that: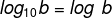
Read too: Decimal logarithm system
Do not stop now... There's more after the advertising ;)
How to calculate a logarithm?
To calculate a logarithm, we have to look for a number that, when we raise the base, results in the logarithm. Taking as an example the logarithm of 36 in base 6 in the previous example, we should find a number that, when we raise base 6, results in 36. like 62 = 36, with answer 2. Let's look at more examples:
1) Log 1000. To calculate this logarithm, we must find a number that, raised to 10, is equal to 1000, that is, 10x = 1000.
Solving the exponential equation, we have:
10x=1000
10x = 103
x = 3
Therefore,

1.Calculate the logarithm:
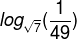
We must find a number which, to the root of 7, is equal to one forty-nineths. Solving the equation, we have:
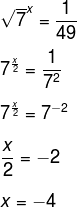
read more: Exponential equation - equation with unknown in exponent
Logarithm existence condition
Consider the following logarithm:
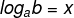
The expression is only defined for when the base is greater than zero and different from one and when the base is greater than zero, that is:
a > 0 and a ≠ 0
b > 0
Ownership of logarithms
See the main ones below. properties of logarithms. All logarithms quoted here satisfy the existence condition.
Property 1
The logarithm of the product of two factors is equal to the sum of the logarithms of these factors.

Property 2
The logarithm of the quotient between two numbers is equal to the difference of the logarithms of those numbers.
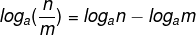
Property 3
The logarithm of a power is equal to multiplying the exponent of that power by the logarithm of the base of the power, where we keep the base of the logarithm.

Property 4
The logarithm of a root is equal to the inverse of the index of the root multiplied by the logarithm, where we also keep the base.
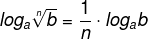
Property 5
The logarithm of a number, in a base raised to a power, is equal to the multiplication of the inverse of the exponent of that base.

Know more: Applications of theogarithms: see examples
solved exercises
question 1 - (Fuvest - SP) If x5 = 1000 and b3 = 100, so the logarithm of x in base b is:
A) 0.5
B) 0.9
C) 1.2
D) 1.5
E) 2.0
Solution
Since the numbers 1000 and 100 can be written in base 10, we have:

Substituting the logarithm of x into base b and applying the definition, we have:
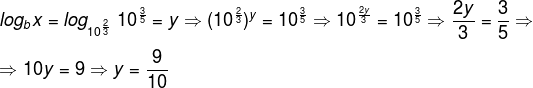
question 2 - (Enem) The hydrogenic potential (pH) of a solution is defined as the index that indicates its acidity, neutrality or alkalinity. It is found as follows:
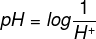
being H+ the concentration of hydrogen ions in that solution. The pH of a solution, where H+ = 1,0 ·10-9, é:
Solution:
Replacing the H value+ in the pH formula, we have:
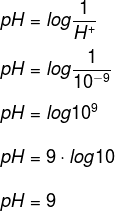
By L.do Robson Luiz
Maths teacher


