sine and cosine in supplementary angles are knowledge used for calculations involving Trigonometry on a triangleany. To understand this, remember that sine and cosine are set to right triangles, more specifically for the two angles sharp edges of these triangles. Thus, the values of sine and cosine are initially set only for acute angles (less than 90°).
THE Trigonometry can be expanded to triangles that are not rectangles, through sins law and of the cosine law. However, these triangles must be obtuse angles, and we must calculate the sine it's the cosine just from that angle. In this case, we will use the sine and cosine of supplementary angles, obtained through the trigonometric cycle.
Sine of supplementary angles
the values of the sine of two anglessupplementary are always the same. This happens because of the knowledge added to the Trigonometry with the use of trigonometric cycle.
Through the trigonometric cycle, it is possible to determine the sine from angles greater than 90°. To do so, just build the angle in question, following the rules of
cycletrigonometric, and observe what is the value of sine connected to that angle.
As an example, the angle of 150° is connected to point D, and the length of segment CD is equal to 0.5 cm. In the first quadrant, the angle connected to this same measurement is 30°, since sin30° = 0.5. Hence, sin30° = sin150°.
thinking of a angleany, representing it by α and assuming that this angle is obtuse, we can represent it as follows in the cycletrigonometric:
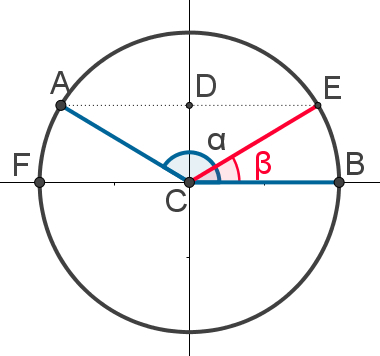
In the image above, angles α and β are connected to the same point D, on the axis of sines. This means that sinα = β. Note that α is equal to the difference between the BF arc and the FA arc. As FA = EB = β, we will have:
α = BF - β
Note that BF = 180°, therefore:
α = 180° – β
Therefore, we will have:
sinα = sin (180° – β)
Since α and β are supplementary, then we can say that the sines of anglessupplementary they are the same.
Observation: Note that this rule only serves to find out which angles have equal sine, as they are supplementary. this rule no can be used to subtract sines from two angles.
Cosine of two supplementary angles
Making calculations analogous to the previous ones, we can conclude that the cosines of two anglessupplementary are additive inverses, that is:
cosα = – cos (180° – β)
or
– cosα = cos (180° – β)
These two expressions can be used, for example, to determine sine and cosine from angles like 135°:
sinα = sin (180° – β)
sin135° = sin (180° - 135°)
sin135° = sin (45°)
sin135° = √2
2
– cosα = cos (180° – β)
– cos135° = cos (180° – 135°)
– cos135° = cos (45°)
– cos135° = √2
2
cos135° = – √2
2
by Luiz Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/seno-cosseno-angulos-suplementares.htm
