The trigonometric ratios secant, cosecant and cotangent are inverse of the reasons cosine, sine and tangent. The study of trigonometry in trigonometric cycle obtained great contributions to the development of inverse functions
The inverse sine ratio (sin x) is known as the cosecant (cossec x), the inverse cosine ratio (cos x) is known as the secant (sec x), and the inverse ratio of the tangent (tg x) is known as the cotangent (cotg x). They can be represented by:

Read too: The 4 most made mistakes in basic trigonometry

cosecant
Known as the trigonometric ratio sine inverse, the cosecant is set to angles whose sine is nonzero. To find the cosecant of a angle x, we just have to calculate the inverse of its sine value.
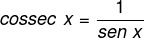
Example
Calculate the value of cossec 60º.

Do not stop now... There's more after the advertising ;)
Cosecant in the trigonometric cycle
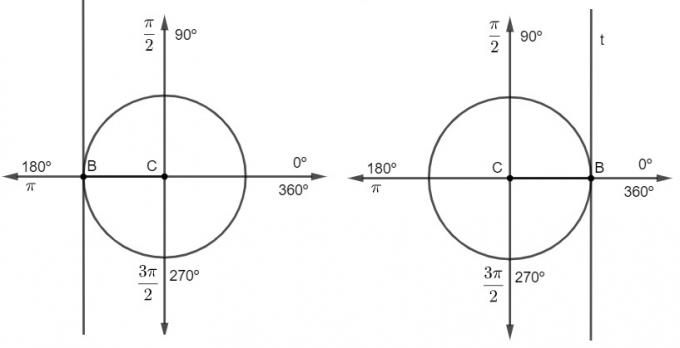
In the study of trigonometry, the cosecant ratio is linked to the trigonometric cycle, which is a circle of radius 1. To find the cosecant of an angle geometrically, knowing the angle x, let's draw the line tangent to point B, line t. The cosecant of x will be the
segment connecting the center to the point where the line t intersects the vertical axis, represented by AC in the image.
Condition of existence of the cosecant
As we saw that the value of the cosecant is the segment that connects the center of the circle to the point where the tangent line touches the vertical axis, we realize that there are three angles where there is no definite cosecant, as the tangent line does not touch the vertical axis.
There is no cosecant for the angles of 0º, 180º and 360º. Let's remember that at these angles the sine value is zero, algebraically, we would be calculating the division of 1 by zero, which is not possible.
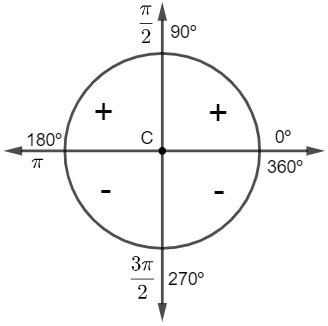
cosecant sign
It is possible to see, in the representation in the cycle, that for angles greater than 0º and less than 180º, the cosecant will always be positive. for angles above 180º, the sign of the cosecant will be negative, that is, the cosecant is positive in the 1st and 2nd quadrants and negative in the 3rd and 4th quadrants.
See too: Reduction to the first quadrant in the trigonometric cycle
drying
known as the cosine inverse trigonometric ratio, the secant is defined for angles whose cosine is nonzero. To find the secant of an angle x, we just need to calculate the inverse of its cosine value.
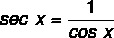
Example:
Calculate the 45° sec.
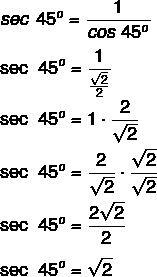
Secant in the trigonometric cycle
To find the secant of an angle geometrically, knowing the angle x, let's draw the line t, tangent to point B. The secant of x will be the segment connecting the center to the point where the line t intersects the horizontal axis, represented by CD in the image.
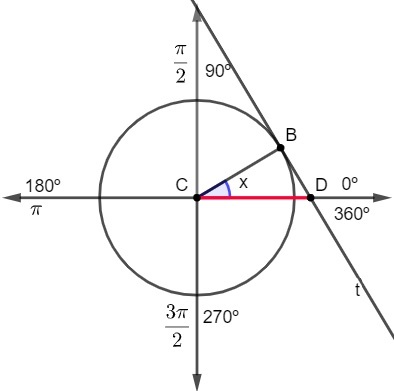
Condition of existence of the secant
There is no secant for the angles of 90º and 270º, geometrically, because at these points the line t does not touch the axis horizontally and algebraically, because the cosine value of 90° and 270° is zero, and the division of 1 by zero is impossible.

secant sign
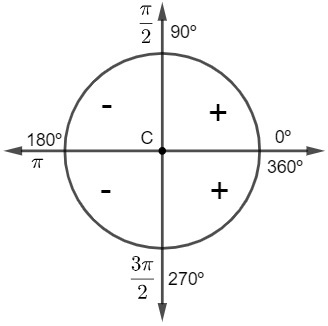
For angles larger than 0º and smaller than 90º and for angles larger than 270º and smaller than 360º, the secant will always be positive. For angles above 90º and smaller than 270º, the sign of the secant will be negative, that is, the secant is positive in the 1st and 4th quadrants and negative in the 2nd and 3rd quadrants.
See too: Applications of Trigonometric Laws of a Triangle: Sine and Cosine
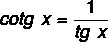
Cotangent
known as the inverse trigonometric ratio of tangent, the cotangent is defined for angles whose tangent is non-zero. To find the cotangent of an angle x, we just need to calculate the inverse of its tangent value.
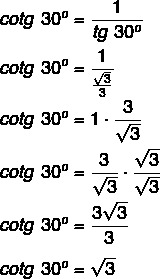
Example:
Calculate the 30º cotg.
Cotangent in the trigonometric cycle
To represent the cotangent, we draw a line p, parallel to the horizontal axis at point A. Then, when constructing the angle x, we draw the line r, which passes through the center C and through the point B, to find the point E, which is the meeting point between the lines p and r. Track AE will be the cotangent of angle x.

Cotangent existence condition
the cotangent does not exist for angles whose tangent is equal to zero, which are the angles of 0º, 180º and 360º. Geometrically, at these angles the line r will be parallel a p, so they have no common point, which makes it impossible to trace the segment AE.

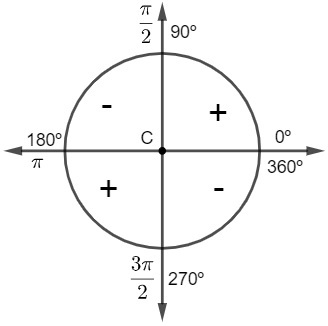
cotangent sign
The sign of the cotangent is positive for angles greater than 0º and smaller than 90º and also for angles greater than 180º and smaller than 270º, and is negative for angles greater than 90º and smaller than 180º and also for angles greater than 270º and smaller than 360º. So the cotangent it is positive for the 1st and 3rd quadrants (odd) and negative for the 2nd and 4th quadrants (even).
Solved Executions
question 1 – The trigonometric functions cotg x and sec x in the second quadrant have images, respectively:
a) positive and positive
b) negative and negative
c) positive and negative
d) negative and positive
Resolution
Alternative B.
Analyzing the behavior of each of the functions, it can be seen that the cotangent is positive in the odd quadrants and negative in the even quadrants, so it will be negative in the 2nd quadrant. The secant function is positive in the first and fourth quadrants and negative in the second and third quadrants, so it will also be negative.
question 2 - Knowing that x = 90º, the value of the expression is:
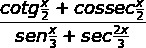
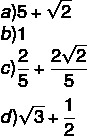
Resolution
Alternative C.
Substituting x = 90º, we have that:
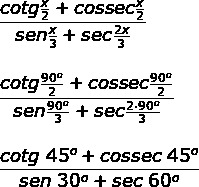
Now let's separately calculate each of the trigonometric ratios:
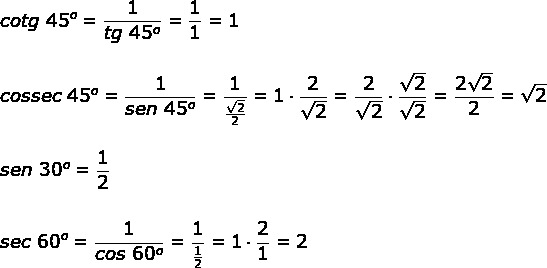
By calculating each one of them, it is possible to substitute in the expression:
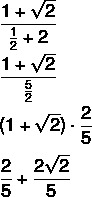
By Raul Rodrigues de Oliveira
Maths teacher