Pyramids they are polyhedra built from a base polygonal and a point outside the flat where is that base. They are three-dimensional and therefore they can only be defined in a space that has three or more dimensions. The formal definition of pyramids is as follows:
One pyramid is the set of straight segments whose endpoints are a polygon and an out-of-plane point that contains that polygon. Look:
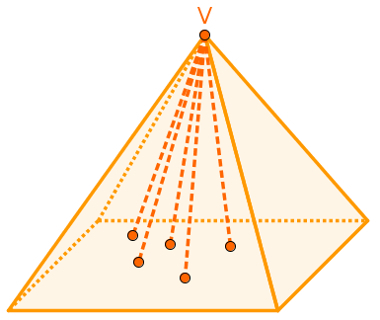
Elements of a Pyramid
as the pyramids are geometric solids basically formed by straight line segments, we can find in them some elements, namely:
faces: are the polygons that can be observed in this polyhedron;
Edges: are the straight lines formed at the intersections of the faces;
vertices: are the meeting points between the edges;
Vertexgivespyramid: is point V in the figure above;
Base: polygon used in the definition of the pyramid;
Edgesgivesbase: edges that belong to the base;
Edgessides: edges that do not belong to the base of the pyramid;
facessides: faces of pyramid that are not your base;
Heightgivespyramid: distance between the vertex of the pyramid and the plane that contains its base;
-
Sectioncross: intersection of pyramid with a plane parallel to the base;
Do not stop now... There's more after the advertising ;)
Apothem: height of a side face in relation to the base of a pyramid regular.

classification of a pyramid
At pyramids can be classified according to their number of faces. Note that this number always equals the number of sides of the base added to one unit. Also note that, except for the base of the pyramid, all faces are triangular.
Pyramidtriangular: has a triangle as a base;
Pyramidquadrangular: has a quadrilateral as a base;
Pyramidpentagonal: Has a pentagon as a base.
And so follows the classification, which depends on the number of edges of the base of the pyramid. It is noteworthy that the triangular pyramid is also called a tetrahedron.
regular pyramid
One polyhedron é regular when is a Plato's polyhedron and, simultaneously, their faces are congruent and regular polygons.
In the specific case of pyramid, the regularity can also be verified as follows: if the base is a regular polygon and the straight segment representing the height has the center of the base as the second end, the pyramid é regular.
The ownership of pyramidsregular is as follows: side edges are congruent and side faces are isosceles triangles.
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "What is a pyramid?"; Brazil School. Available in: https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-piramide.htm. Accessed on June 27, 2021.