Polynomials are algebraic expressions formed by adding monomials.. Both are made up of known numbers and unknown numbers. Before moving on to the mathematical operations involving polynomials, we need to better understand some concepts. Come on?
→ What are monomials?
monomials they are made up of the product of known and unknown numbers (unknown numbers commonly represented by letters). Unknown divisions are not considered monomials, but they are called algebraic fractions.
Examples:
a) 4x
b) 7xy2
The known number is called the coefficient, and the rest of the monomium is called literal part. If analyzed within a polynomial, the monomium is also called a term. A term is generally recognized not because of this, but because it is always separated by additions and subtractions. When the literal part of two or more monomials is equal, we say they are similar monomials.
→ Examples of Polynomials
As stated earlier, any algebraic expression formed by the addition of monomials is called a polynomial. Thus, here are the examples of polynomials:
a) 4xy + 2x + 7yw
b) 4x4 – x2 + 60x – 7
→ Addition and subtraction of polynomials
rewrite the polynomials putting similar terms side by side. Add or subtract these terms in the same way we monomials. See an example:
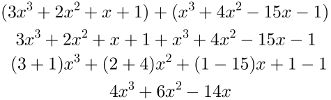
The subtraction of polynomials involves the distributive property of multiplication and modifies all signs of the second polynomial. Only after playing this game of signs can we continue with the subtraction. Watch:
Do not stop now... There's more after the advertising ;)

→ Polynomial Multiplication
THE polynomial multiplication is fully grounded in the distributive property better known as shower. To do this, just multiply each monomium in the first polynomial by all the monomials of the second, observing the signs of the results. For example:

→ polynomial division
For share two polynomials, use the key method, just as you do for integers. Look at the example:
In the division of the polynomial P(x) = x3 + 7x2 + 15x + 9 by the polynomial D(x) = x + 1, P(x) is the dividend, D(x) is the divisor and the result Q(x) is the quotient and is obtained as follows:

First, look for a monomial that, multiplied by the highest-degree term of D(x), has the highest-degree term of P(x) as a result. This monomium is x2.
Finding it, multiply it by D(x) and place the result under P(x), just as you do with whole number division. Watch:

Remember that this result must be subtracted from P(x), so the signs of the result of the previous multiplication must be swapped.

Once this is done, perform the subtraction and "down" all terms that are not subtracted:

Repeat the procedure until the remainder has a degree less than D(x).

By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "What is a polynomial?"; Brazil School. Available in: https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-polinomio.htm. Accessed on June 27, 2021.
Learn the definition of polynomial equation, define a polynomial function, the numerical value of a polynomial, the root or zero of the polynomial, Degree of a polynomial.