At Ohm's laws allow us to calculate important physical quantities, such as voltage, current and electrical resistance of the most diverse elements present in a circuit. However, these laws can only be applied to ohmic resistances, that is, bodies whose resistances have a constant modulus.
→ 1st law of Ohm
THE 1ªlawinOh M determines that the potential difference between two points of one resistor is proportional to electric current which is established in it. Furthermore, according to this law, the ratio of electric potential to electric current is everconstant for resistorsohmics.
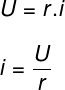
U – Voltage or electrical potential (V)
r – electrical resistance
i - electric current
In the law shown in the figure above, we call it U the electrical voltage or electrical potential. This magnitude is scalar and is measured in Volts The difference in electrical potential between two points on a circuit, in turn, indicates that there is a electrical resistance, as shown in the figure:

When electrical current passes through the resistive element R, there is a drop in electrical potential.
Lookalso: Resistor association
That difference stems from consumptiongivesenergy of the electrons, since these particles transfer part of your energy to the atoms of the crystal lattice, when led by means that present resistance to your driving. The phenomenon that explains such energy dissipation is called joule effect.
Do not stop now... There's more after the advertising ;)
The figure below shows the profile of the electrical potential before and after the current passes through a resistive element of an electrical circuit, observe the power drop:

When electrical current is conducted in a body with electrical resistance, some of its energy is dissipated.
the electric current i measures the flow of charges through the body in Amperes, or in C/s. The electric current is directlyproportional to the electrical resistance of bodies: the greater the electrical resistance of a body, the smaller the electrical current to pass through it.
→ 2nd law of Ohm
The electrical resistance R is a propertyofbody which is traversed by an electric current. This property depends on factorsgeometric, like the length Or the areacross of the body, but it also depends on a quantity called the resistivity. Such magnitude relates exclusively to the material from which a body is formed. The law that relates electrical resistance to these quantities is known as Ohm's second law. Ohm's second law is shown in the figure below:

R – electrical resistance (Ω)
ρ – resistivity (Ω.m)
L – length (m)
THE – cross-sectional area (m²)
We call an ohmic resistor every body capable of presenting constant electrical resistance for a given range of electrical voltages. The graph of voltage versus electrical current for ohmic resistors is linear, as shown in the figure below:

The resistor can be considered ohmic in the range in which its electrical potential increases linearly with electrical current.
Taking the straight segment of the graph, it is known that the electrical potential between the terminals of a resistor will undergo a variation in its electrical potential, which is always proportional to the electrical current that runs through it, as shown in the figure below:

Analyzing the graph shown above, we see that electrical resistance can be understood as the slope of the straight, given by the tangent of angle θ. As we know, the tangent is defined as the ratio between the peccariesopposite and adjacent and, therefore, it can be calculated with the formula R = U/i, in the case where the resistances are ohmic.
See too: 5 Things You Should Know About Electricity
→ Calculation of electric power by Ohm's law
Through Ohm's law, it is possible to determine the electric power which is dissipated by a resistor. Such energy dissipation occurs due to the Joule effect, so when we calculate the dissipated power, we are determining how much electrical energy a resistor is capable of converting into heat, each second.
There are some formulas that can be used to calculate electrical power, check out some of them:

P – Electric power (W)
AND – Energy (J)
t – Time interval(s)
R – Resistance (Ω)
i – Electric current (A)
U – Electric potential (V)
→ Ohm's Law Formulas
Check out the formulas of the 1st and 2nd Ohm's Law:
1st law of Ohm:

2nd law of Ohm:

mallet
There is a trick that can facilitate the use of the 1st law of Ohm. This trick, called the triangle trick, consists of capping the variable we want to discover in the triangle shown below, so that we reveal the formula to be used. Check out:
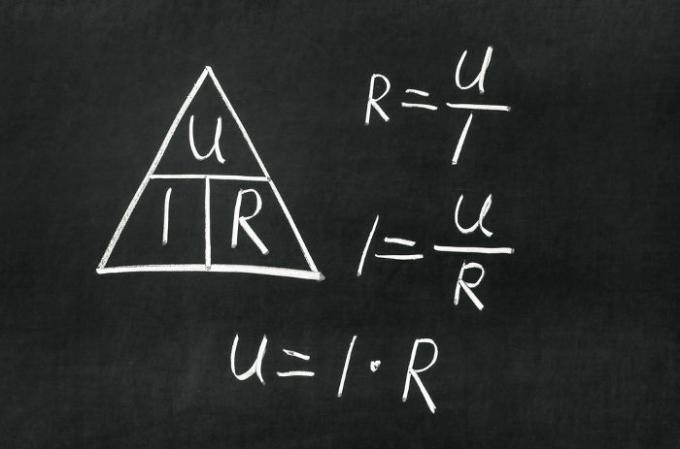
With the mallet of the triangle it is possible to discover the formula to be used
For example, if we want to calculate the electric potential (U), just cap the U in the figure above, so we will see that U is equal to the electric current (i) multiplied by the resistance (R). Similarly, if we cap the electric current (i), we will see that it can be calculated by dividing U by R.
Read too: Physics formula tricks
solved exercises
1) An ohmic resistor, with a resistance equal to 10 Ω, is crossed by an electric current of 1.0 A. Determine the potential drop that an electrical current undergoes when passing through this resistor and mark the corresponding alternative:
a) 5V
b) 25 V
c) 15V
d) 20 V
e) 10 V
Resolution:
To calculate the potential difference that the current suffers when passing through the resistor, we can use Ohm's law. Watch:
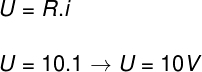
Template: Letter E.
2) When an electrical current of 1.5 mA passes through it, the potential difference at the terminals of an ohmic resistor is 1.5 V. Check the alternative that indicates the modulus of electrical resistance of this resistor:
a) 1.10-³ Ω
b) 1.10³ Ω
c) 1.5.10-3 Ω
d) 2.25.103 Ω
e) 1 Ω
Resolution:
To solve this exercise, we will make use of Ohm's law. Therefore, we need to realize that the electrical current given in the exercise statement was reported in the unit of mA (milliampere), a submultiple of the Ampere that is equivalent to 10-3 A, observe the calculation process:

Feedback: Letter B.
By Me. Rafael Helerbrock