Speedaverage is the variation of the position (displacement) of a mobile in relation to a reference frame during a certain period of time. The unit of measurement of the average speed, according to the SI, is the meter per second (m/s).
Lookalso: Uniformly varied movement (MUV) - summary and exercises
What is average speed?
The average speed is a Vector greatness which depends on the differences between the end and start positions of a move. During a Formula 1 race, for example, cars can develop very high instant speeds, however, at the end of the race, they will have returned to their starting position. In this way, their average speed throughout the entire journey was equal to zero.
Since the average speed depends exclusively on the difference between the positions, it doesn't matter if a body remained stationary most of the time or if it accelerated, for example. Want to learn more? Check out our text about the uniform movement.
Below, we present the formula used to calculate the average speed, note:

vm – average speed (m/s)
ΔS - displacement (m/s)
sF – final position (m)
S0 initial position (m)0s
An important detail about the average speed is that it cannot be confused with the average speeds. This is only possible when the time spent on each part of the route is the same for each of the speeds. This type of average is called: harmonic mean.
Do not stop now... There's more after the advertising ;)
Average speed calculation
Graphically we can understand the average speed as the slope of the straight line of position as a function of time, the more leaning is this straight, the bigger is yours velocityaverage. In this sense, we understand that the average speed is measured by the slope of the straight line.
Know more: Uniform Motion Graphics
Look at the following graph that relates position x to time:

If we want to calculate the average speed of the movement illustrated by the graph, we need to calculate its coefficientangular. For that, let's choose the points of t = 0 s and t = 0.5 s, corresponding to the positions x (t) = 0 m and x (t) = 1.5 m, as shown below:
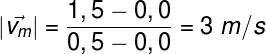
Also access: Exercises about uniform movement? Click here!
By applying the average speed formula, we found that this mobile moves, on average, threemeters every second. Below we graph the position as a function of time for twofurniture different, one of which (in yellow) is accelerated:

Note that, between the instants of time t = 0.0 s and t = 1.0 s, the two mobiles traveled the same distance: x = 2.0 m. So, during this period of time, although they are movementsmany different, the furniture pictured had the same average speed, however, this is no longer true for instants of time greater than t = 1.0 s.
See too:What is the speed of light? Access and discover
Because it is a greatnessvector, O displacement it must be calculated as such, taking into account the difference between the final and initial positions, in the three directions of space. However, in some cases, such as those often presented in books of TeachingAverage, only one is taken into account directionofmovement, so that it is only necessary to subtract the modules of the S positionsF and S0. Check out a solved exercise example about velocityaveragealong a straight:
Example – An automobile leaves a city located on the margins of kilometer 640 of a straight highway. Two hours later, you are at kilometer 860 of that same highway. Determine the average speed of this car.
Resolution:
To calculate the average speed, just assume that the displacement of the car is equal to the total space covered by it: 220 km. Then, we just need to divide this distance and the time needed to cover it:

As well as this situation, there are several exercises in textbooks in which the direction and meaning of the movement, therefore, we speak of average scalar speed, a physical concept that is not very coherent, since all speed is vector. In this case, what must be understood is that these exercises refer to the module or magnitude of velocity.
This average scalar speed is, in turn, defined by the spacetotaltraveledDividedfurbreakintime. We'll talk a little more about the differences between average speed and average speed later.

Average speed and average scalar speed
THE average scalar speed is used to define the how quickly a piece of furniture moves, regardless of the direction and direction of its movement. Therefore, this speed is a particular case of average speed, in which the mobile always moves in the same direction and in the same direction.
The meaning of average velocity, in turn, is much broader, and can refer to the movement of a body in the three directions of space, for example.
Now we present the formula used to calculate the average scalar velocity:

Let's check out an example of using this formula:
Example – A traveler wants to complete a 120 km journey with an average speed of 60 km/h. Knowing that the traveler has covered three quarters of the way at a speed of 50 km/h, how long will it take? travel the rest of the route in order to complete it according to the average speed he had planned?
Resolution:
According to the exercise, the traveler wants to complete his trip with an average speed of 60 km/m. Knowing that the path to be covered is 120 km, it is concluded that the duration of your trip should be 2 h.
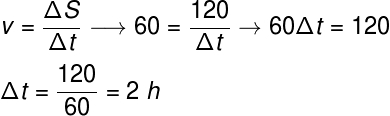
According to the statement, the traveler covered three quarters (¾) of the 120 km journey (ie, 90 km) at a speed of 50 km/h. In this case, we are going to calculate the time taken for that part of the trip.

The result obtained indicates that there are only 0.2 h left to complete the journey, since the total time must be 2.0 h. In addition, as 1 h is 60 minutes, the traveler must end his trip, at most, in 12 minutes.
If requested by the exercise, it is also possible to calculate the average speed that the traveler must develop on the remaining route, for that, just to share the space he hasn't covered by the remaining time, see how:
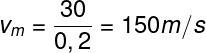
The result obtained indicates that, to complete the route according to the planned average speed, the traveler must move at a speed of 150 km/h.
Lookalso: Find out what you should study about Mechanics for the Enem exam
Average vector speed
THE vector speed average should be calculated according to rules ofsumvector.
In the figure we show the positions (x0yy0) and (xFyyF) of a mobile in relation to the reference (0,0):
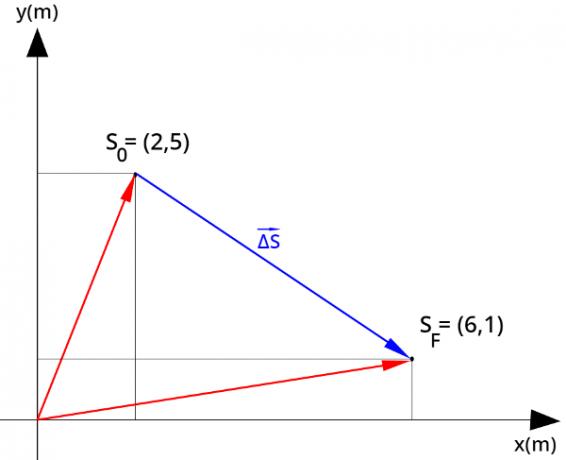
The figure shows a two-dimensional movement, in which a mobile starts from position S0 (2, 5) and moves to position SF (6, 1), thus, its displacement, that is, the difference between the final and initial positions, was (4, -4). The red arrows are the position vectors, which locate the object in relation to the frame (0,0).
Let's assume that this displacement has occurred in a time interval equal to 2.0 seconds, in this case, to calculate the modulus of the average vector velocity, it is necessary to determine the vector moduledisplacement, which can be obtained by the Pythagorean theorem, since the x and y directions are perpendicular to each other:

After determining the displacement module, just use the formulagivesvelocityaverage, dividing the result by the time interval in which the movement occurred:
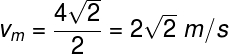
Average speed summary
Speedaverage is the reason between the displacement it's the breakintime where a movement happens.
Displacement is greatnessvector, measured by difference between the positionsFinal and initial of a movement.
THE velocityaverage cannot be confused with the averageof thespeeds, this is only possible if the time intervals in which a mobile remained at each of the speeds are equal.
Speedaverage é different in average scalar speed, the latter is a particular case, in which a mobile moves in a straight line, in a single direction and direction.

Solved exercises on average speed
Question 1) A Formula 1 car travels a 1.0 km long circular track, taking 20 seconds to complete a lap, after starting from the start, which also marks the end of a lap. The alternative that correctly displays the average speed module of this vehicle over a full lap is:
a) 50 m/s
b) 0 m/s
c) 180 m/s
d) 20 m/s
e) 45 m/s
Template: Letter B
Resolution:
To solve this exercise, just remember that the average velocity is vector and depends directly on the displacement, which, in this case, is equal to zero, since, having completed a lap, the car is in the same position from which it started, so its average speed is equal to zero.
Question 2) To place a parcel, a delivery person travels two blocks north and three blocks east, within a 15-minute time span. Disregarding the length of the streets and taking into account that the length of each block is 50 m, determine the average speed and the average speed, in km/h, developed by the postman.
a) 0.7 km/h and 3.6 km/h
b) 2.5 km/h and 4.0 km/h
c) 5.0 km/h and 4.0 km/h
d) 2.0 km/h and 1.0 km/h
e) 0.9 km/g and 2.7 km/h
Template: Letter a
Resolution:
According to the exercise, the delivery person moves three blocks to the east and two blocks to the north, with the length of each one of these blocks being 50 m. Thus, we know that the total space covered by the delivery person is 250 m (0.25 km), as he passed through five different blocks.
With the information obtained so far, such as the total space traveled (250 m) and the transfer time (15 minutes = 0.25 h), it is easy to calculate its average scalar velocity:

The average velocity, in turn, is a little more complex. In order to calculate it, it is necessary to determine what was the vector displacement of the postman. In this case we know that the postman moved 150 m in the horizontal direction (heading east) and 100 m in the vertical direction (heading north). To obtain its displacement, it is necessary to apply the Pythagorean theorem, note:

Finally, to find out the speed of this delivery person, we divided the distance traveled by the total time in seconds:

Gathering the information obtained, we have that the average vector speed of the delivery man is 0.7 km/h, while his average speed is 3.6 km/h.
By Rafael Hellerbrock
Physics teacher

