Movementevenlymiscellaneous (MUV) is a movement in which the change of speed, called acceleration, occurs at a constant rate. The uniformly varied movement is a particular case of themovementmiscellaneous. In this one, the speed only varies, while in this one the speed variesinmannerconstant, that is, its magnitude undergoes equal increases or decreases every second.
Lookalso: Everything you need to know about Newton's laws
Introduction to uniformly varied motion
When a piece of furniture develops a uniformly varied movement, its speed increase or will steadily decrease, every second. When this speed increases, we say that its movement is accelerated; when it decreases, we say its movement is retarded.
The uniformly varied movement can be described by means of hourly functions, similar to those used for uniform movement, being more general. Also, to solve some exercises related to this type of movement, it is necessary to understand the meaning behind the graphics of position and velocity. Therefore, we are going to study the different MUV time functions as well as their respective graphical representations.
Do not stop now... There's more after the advertising ;)
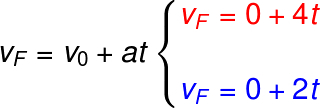
First, we'll deal with the hourly velocity function, which can also be written in the form of the formula used to calculate the average acceleration, see:
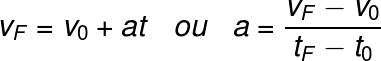
vF and you0 - final and initial speeds (m/s)
The - acceleration (m/s)
t - time interval(s)
The formula shows that the speed of a rover varies linearly with its acceleration, that is, assuming a body has an acceleration of 3 m/s², its velocity will increase by 3 m/s each second.
If we pay attention to the format of the position's hourly function, we will see that it is a first degree function like y = a + bx, known as straight equation. In the case of the hourly velocity function, the coefficient a, called linear coefficient, and the initial speed of the mobile, while the coefficient b, known as angular coefficient, and the acceleration of this piece of furniture.
In the following figure we bring a graph of velocity as a function of time v (t), check:
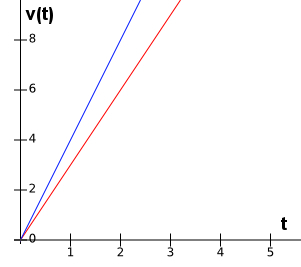
In the graph, we see two lines, one red and one blue, which represent the movement of two pieces of furniture. These depart from home (v0 = 0) and start to accelerate steadily. One second after its departure, the blue rover is at a speed of 4 m/s, while the red rover is at 2 m/s. Analyzing the slope of the straight lines, it is easy to see that the acceleration of the blue rover is greater than that of the red rover.
See too:Check out amazing facts about the Solar System
It is possible to see, based on the reading of the graph, that the speed of the mobile in blue increases by 4 m/s, every second, while the speed of mobile B increases by only 2m/s, for the same interval of time. In this way, we can write the hourly functions of the movements represented by the blue and red lines, check:
Below, we show what the format of the chart of a accelerated uniformly varied motion and retarded in red and blue, respectively. For both, we will adopt an initial non-zero speed:
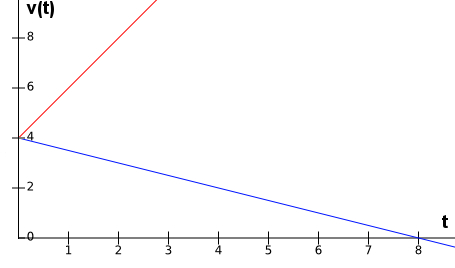
Note that the delayed movement, represented by the blue line, reverses its meaning at time t = 8 s, since its velocity starts to assume negative values.
Lookalso: Learn to solve exercises on uniform movement
In addition to getting the mobile acceleration, based on the velocity graphs, it's also possible that calculate the distance traveled by the mobile. For this we must calculate the area of the graph below the line. This area can be easily found considering the trapeze area and can be obtained directly by the following formula, especially useful for when the mobile acceleration is not known:
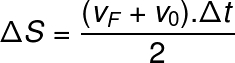
In addition to the hourly speed function, the MUV uses position hour functions. These are second-degree functions, since the displacement of a mobile in MUV is proportional to the squared time interval. Now check the position and displacement equations for the MUV:
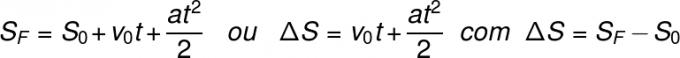
sF - final position
s0 - starting position
v0 - initial speed
S - displacement
Such equations resemble second-degree functions of type ax² + bx + c = 0. In these hourly functions of position and displacement, O coefficientTheequals à a/2 (acceleration divided by two), which multiplies the term t², while the velocityinitial (v0) represents the coefficientB.
Based on this, we will show you how the uniformly varied motion graphics look for the accelerated, in red, and delayed, cases in blue, starting from a non-zero initial velocity:

Analyzing this graph, it is possible to see that, for the accelerated movement, in red, the concavity of the parabola is facing upwards, since its acceleration is positive, while for the delayed movement, in blue, the concavity of the parabola is turned downwards, because its acceleration presents the opposite direction to its initial velocity.
The hourly functions that were used to form the graphs, represented by the red and blue curves respectively, as well as their values of position, velocityinitial and acceleration are shown below:

Torricelli Equation
THE Torricelli equation is very useful when we need to solve a problem related to movementevenlymiscellaneous and we don't know at what time interval it occurred. This equation can be easily obtained based on the hourly functions of position and velocity.
Check out the formula for the Torricelli equation:
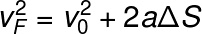
If you are more interested in the topic, read our text: Torricelli Equation.

Lookalso: Find out why man has not returned to the moon
solved exercises
Question 1) A mobile moves with an initial speed of 20 m/s, when it starts a braking process, with a deceleration of 2.5 m/s². Determine the time needed for this piece of furniture to reverse its direction of movement.
a) 8.0 s
b) 50.0 s
c) 5.0 s
d) 10.0 s
e) 12.5 s
Template: Letter a
Resolution:
To solve this exercise, we will make use of the hourly velocity function. In this sense, we can say that the mobile will invert the direction of its movement in the instant following that in which its speed becomes null. Thus, we will find the time needed for the final speed of this mobile to be 0 m/s, knowing that its initial speed was 20 m/s:

In this calculation, we used the negative sign for acceleration due to the fact that the mobile had its speed decreased every second, which characterizes a delayed movement.
Question 2) A rover has its hourly displacement function given by S = 5 + t². Check the alternative that indicates the initial velocity and acceleration of this rover, respectively:
a) 5 m/s and 1 m/s²
b) 0 m/s and 2 m/s²
c) 1 m/s and 5 m/s²
d) 5 m/s and 2 m/s²
e) 3 m/s and 5 m/s²
Template: Letter B
Resolution:
We know that the hourly shift functions follow the format ax² + bx +c = 0, but we also know that coefficient b equals the initial velocity of the mobile and that coefficient a equals half of its acceleration. Thus, we have to: v0 = 0 and a = 2 m/s².
Question 3) In a graph of position versus time, the curve is seen to describe a parabola with its concavity facing downwards. For this graph, tick the correct alternative:
a) It is an accelerated movement.
b) This is the graph of a retrograde movement.
c) This is the graph of a delayed movement.
d) This is a variable acceleration graph.
e) This is an increasing velocity graph.
Template: Letter C
Resolution:
When the graph of position versus time is in the form of a parabola, we know that this movement has constant acceleration. What tells us if the movement represented by the graph is retarded or acceleratedis the concavity of the parable, which in this case is face down. Therefore, the graph in question represents a delayed movement.
By Me. Rafael Helerbrock