entropy is a greatnessthermodynamics associated with irreversibility of the states of a physical system. It is commonly associated with the degree of "disorder” or “randomness” of a system. According to one of the statements of 2nd Law of Thermodynamics:
“In a thermally isolated system, the measurement of entropy must always increase over time, until reaching its maximum value.”
In other words, the entropy is able to measure the meaning of "arrow of time” of a system. When we see the images below, we intuitively know that the initial state of the system is represented by the image of the left, of the greatest organization:
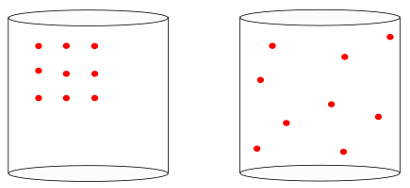
Looking at the previous image, we know that the most likely final configuration is the one in which atoms have speeds in all directions, as well as random positions. That's what entropy is all about: a multiplicity of states of a system must always increase.
Examples
Which of the settings below is more probable to be observed for an arrangement of bricks over time?

In the first configuration, the
multiplicity of the states of the blocks is little: they are all arranged in the directionhorizontal, parallel each other. With the passage of time or the action of an agent, it is expected that its configuration grow up in number in States, favoring the Mondayconformation, illustrated in the image on the right. Other examples can be given:-
When an ice pack is placed in a container with biggertemperature, its temperature increases until it reaches the thermal balance. At that point, the ice can melt. By taking heat again from the ice block, which is now in the state liquid, it can become solid again, but its conformation will not have the same organization that previously presented.
Do not stop now... There's more after the advertising ;)
When opening a bottle of perfume, the heat can help diffusion of your molecules, spreading the contents of the perfume over the entire length of a room. The opposite cannot be expected, since the removal of heat would not promote the return of the molecules into the flask.
Mathematical definition of Entropy
THE mathematical definition of entropy is given by the ratio of the amount of heat (Q) transferred between two portions of a thermally insulated system, in joules (J), by its absolute temperature, in Kelvin (K):

S = Entropy (J/K)
ΔQ = Amount of heat (J)
T = Absolute temperature (K)
The definition given above is valid for isothermal processes, that is, in which there are heat exchanges so small (or slow) that they are not able to change the temperature of the system. The definition of entropy is therefore infinitesimal (infinitely small part).
We can also understand the concept of entropy as follows: being a system formed by two portions of the same gas, in many differenttemperatures, it is possible to extract some amount of work of him moving some piston or hand crank, for example. However, over time, the parts of this gas will tend to balancethermal. If there is no longer a difference in temperature, even with all the energy present there, it will not be possible to extract any workuseful from him.
By Rafael Hellerbrock
Graduated in Physics
Would you like to reference this text in a school or academic work? Look:
HELERBROCK, Rafael. "What is entropy?"; Brazil School. Available in: https://brasilescola.uol.com.br/o-que-e/fisica/o-que-e-entropia.htm. Accessed on June 28, 2021.

