Power is a scalar physical quantity measured in watts (W). It can be defined as the job completion rate every second or as power consumption per second. The watt, the International System of Units (SI) power unit, equals 1 joule per second.
See too:What is mechanical work?
Power and yield summary
power is the rateinvariation the amount of energy supplied or given up by a system over a period of time.
The unit of power in the international system of units (SI) is the watt: 1 watt equals 1 joule per second.
If one machine is able to do the same job as another in a shorter amount of time, its power is considered to be greater than that of the other machine.
The efficiency of a system is given by the ratio between the useful power and the total power.
The power not useful to the system is called potencydissipated.
What is power in physics?
power is a physical quantity used to calculate the amount of energy granted or consumed per unit of time. In other words, it's the rate of variation of energy as a function of time. Power is useful for measuring how quickly a form of energy is transformed by performing a
work.| We say that a machine is more powerful than other machines when it is able to do the same task in a shorter time or even perform a greater number of tasks in the same interval of time. |
the definition of potencyaverage is given by the work performed as a function of time variation:

Subtitle:
P – average power (W)
τ – work (J)
t – time interval(s)
The power measurement unit adopted by the SI is the watt (W), unit equivalent to joulepersecond (J/s). The unity watt was adopted from 1882 as a form of homage to the works developed by JamesWatt, which were extremely relevant to the development of steam engines.
In physics, work is the measure of the transformation of an energy form in other forms of energy through the applicationinonestrength. Thus, the definition of power may be related to any form of energy, such as: energy mechanics, energy potentialelectric and energy thermal.
Power calculation
We can determine the power realized by applying a force F that displaces a mass body m at a distance d. Watch:

In the situation described above, we can calculate the power of the movement by defining the average power:

For that, we need to remember that the workaccomplished by a force F can be calculated using the following formula:
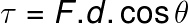
Subtitle:
F – applied force (N)
d – distance covered (m)
θ – angle formed between F and d (º)
Combining the two previous equations into one, we will have the following equation for calculating the power related to a form of energyany:

For cases where the applied force is parallel to the distance traveled by the body, the cosine of the angle θ will have its maximum value (cos 0º = 1). Therefore, the average power can be calculated from the following relationship:

Subtitle:
v – body speed (m/s)
According to the calculation shown above, it is possible to calculate the power with which the energy present in a body is transformed. This is possible if we know the modulus of the resulting force, which should be multiplied by the velocityaverage traveled by the body over a distance course d. However, it is necessary to remember that the definition presented above is only valid for constant values of F.
See too: Exercises on mechanical power and performance
→ Instant power
powerinstant is the measure of the amount of work done in a process over a very small (infinitesimal) time span. We can say, therefore, that the instantaneous power is the rate of change of the quantity of work during a time interval that tends to zero.

Subtitle:
Purge – instantaneous power (W)
Δτ – infinitesimal work (J)
Δt – infinitesimal time interval(s)
Instantaneous power is used to calculate the rate at which work is done at each instant, not during a long process. Therefore, the shorter the time intervals Δt, the more accurate the measurements of the potencyinstantaneous.
mechanical power
powermechanics is defined as the rate of change of energy forms related to the stateinmovement of a body. We can calculate the mechanical power of a moving body through the variations of your kinetic energy and of yours potential energy (gravitational or elastic, for example). The power associated with the transformation of mechanical energy, however, only applies to systemsdissipative (which have friction), since, in the absenceinfriction and others forcesdissipative, The mechanical energy of bodies remains constant.
According to Work-Energy Theorem, it is possible to calculate the amount of work applied to a body by the variation gives energykinetics obtained by him.
the mass body m illustrated in the figure below is accelerated by the action of a force F, having its speed varied from v0 until vF:

Subtitle:
v0 – initial speed (m/s)
vF – final speed (m/s)
According to Work-Energy Theorem, the work performed on the body is given by:

Subtitle:
ΔK – kinetic energy variation (J)
KF –final kinetic energy (J)
KI -initial kinetic energy (J)
m – body mass (kg)
Thus, the potencymechanics related to this movement can be calculated using the following equation:

Electric power
THE potencyelectric it is an important measure that must be analyzed when purchasing a home appliance. The electrical power of any device measures the amount of electrical energy that the device is capable of transforming into other forms of energy each second. For example, a 600 W blender is capable of transforming 600J of electricity every second in energykinetics, broadcasting heat,vibration and wavessonorous for your shovels.
As we know, in general, power can be calculated through the ratio between the work performed and the time interval elapsed during its performance. Therefore, we will use here the definition of work performed by forceelectric:
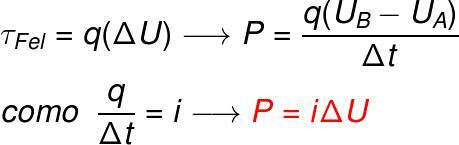
Subtitle:
τGall– work of electrical power (J)
what – electrical load module (C)
ΔU – potential difference (V)
P – electrical power (W)
UB and UTHE -electrical voltage at points A and B (V)
Δt – load movement time interval(s)
i – electric current module (A)
Electric power works as follows: when we plug an appliance into the socket, a differenceinpotential (ΔU) between your terminals. When a potential difference (U) is applied over a conductive material, a the amountinwork(τGall)is performed on the loadselectric (q) in the circuits of the device, causing these loads to move, that is, assigning them energykinetics. THE movementof theloads in a preferred direction is called chainelectrical (i). THE potencyelectric (P), in turn, is the measure of the amountinwork(τGall) which was carried out by the loads to eachsecond (t) operation of the device.
Do not stop now... There's more after the advertising ;)
The consumption of electricity, therefore, is determined by the potency of appliances connected to the electrical network and by its time in operation.
In addition to the formula mentioned above, there are variations that can be written from the 1st Law of Ohm. Are they:
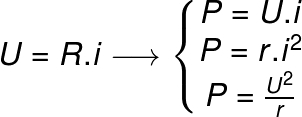
Three Possible Ways to Calculate Electrical Power
Subtitle:
U – electrical potential (V)
r – electrical resistance (Ω)
Lookalso: Power dissipated in a resistor
→ Electricity consumption
the amount of electricity consumed is measured in a unit called the kilowatt hour (kWh). This is an alternative unit to the energy unit of the international system of units, the joule. The kilowatt-hour is used because of its practicality. If electricity were measured in joules, the numbers used to express its consumption would be huge and impractical.
A kilowatt hour is the amount of energy consumed (or the work performed) by an apparatus of 1000W (1 kW) during the time interval of 1h (3600 s). Multiplying these quantities, we come to the conclusion that each kilowatt hour equals 3.6.106 J (threemillions and six hundredthousandjoules).
To calculate the consumption of an electronic device, we simply multiply its power by its operating time.
Example
Consider an appliance of power equal to 100 W (0.1 kW) that operates during 30 minutes a day (0.5 h). what will be yours consumptionmonthly (30 days) of electricity?

According to our calculation, this device will consume 1.5 kWh monthly, the equivalent of 5,4.106 J. If the kWh of the region cost BRL 0.65, the price to be paid at the end of the month for the operation of this device will be BRL 0.97.
Lookalso: Electric generators and electromotive power
Solved exercise of electrical power and yield
When connected to a circuit, a battery with an electromotive force equal to 20.0 V and an internal resistance of 1.0 Ω produces an electrical current of 1.5 A. In relation to this battery, determine:
a) The electrical potential difference established between the terminals of this resistor.
b) The electrical power supplied by the battery.
c) The electrical power dissipated by the battery's internal resistance.
d) The performance of this battery.
Resolution
Initially, we will list the data provided by the exercise.
Data:
UT= 20.0 V - battery electromotive force or total potential
r = 1.0 Ω - internal battery resistance
i = 1.5 A - electric current
a) To determine the potential difference formed between the ends of the resistor, we use the 1st law of Ohm.

Subtitle:
UD – Electrical voltage dissipated in the resistor (V)
B) The electrical power supplied by the battery can be calculated using the formula below:

Subtitle:
UT – total electrical voltage or battery electromotive force (V)
c) Let's calculate the electrical power dissipated by the resistor. For this, we just use one of the potency formulas we already know:

Subtitle:
PD – dissipated power (W)
d) The income of this generator can be calculated using the ratio between the potencyusable and the potencytotal of the battery. From the calculations performed in the previous items, we determined that the total power supplied by the battery was 30 W, while the power dissipated by its internal resistance was 2.25 W. Therefore, the usable power is given by the difference between these two powers and is worth 27.75 W. By making the ratio between usable power and total power, we will have:

According to the calculation performed, the battery's energy yield is 92.5%.
Thermodynamic Power
Thermodynamic power can be calculated by determining the the amount in work which is performed by (or over) a gas during its expansion or compressionisobaric (constant pressure) for a period of time.
It is also possible to calculate the potency of a sourceinheat relating the amount of sensible or latent heat emitted by time interval.
→ Power of the work performed by the gas
In isobaric transformations, it is possible to determine the power supplied or transferred by a gas. To do so, we need to take into account the formula used to calculate the workthermodynamic involved in a transformationisobaric:

Subtitle:
Pr – pressure (Pa)
Pot – power (W)
ΔV – volume variation (m³)

In isobaric thermodynamic transformations, the gas converts some of its internal energy into work by pushing a piston.
Lookalso: The history of thermal machines
→ Power and heat
We can determine the potency supplied by a flame or the power emitted by a resistor heated as a result of the It is madeJoule by calculating the amount of heat dissipated by these sources every second. To do so, just do the following calculation:

To calculate the power emitted by a source in the form of heat, just determine if this heat is of the type sensitive (Q = mcΔT) or of type latent (Q = mL). These heats are present exclusively in the changesintemperature and in the changesinstatephysicist, respectively.
Performance
Performance it is an important variable for the study of non-conservative systems, that is, those that present energy losses, as in the non-ideal cases of our daily life. All machines and devices that we know of are systems incapable of harnessing all the power supplied to them. Thus, they "waste" part of the power in other less useful forms of energy, such as heat,vibration and noises.
One of the most general definitions of efficiency can be given by dividing the useful power by the total power received during some process:

Subtitle:
η - Yield
PU – useful power (W)
PT – total power (W)
Yield of a machine
O Yield of thermal machines measures their energy efficiency, that is, the percentage of energy that these machines are able to use to perform useful work (τ). All thermal machines operate in a similar way: they receive heat from a hot source (Qwhat) and reject part of this heat, dissipating it to a cold source (Qf).
We can calculate the Yield of any thermal machine from the following formula:
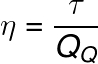
Subtitle:
η – efficiency of the thermal machine
τ - work of the thermal machine (J)
Qwhat – heat given up by the hot source (J)
The above list can be written in another way. For this, we just assume that the useful work (τ) is given by difference between the amount of heat given up by the sourcehot (Qwhat) and the amount of heat dissipated to the sourcecold (QF):

Subtitle:
QF – heat given up by the cold source (J)
→ Carnot machine performance
O cycleincarnot it's a thermodynamic cycle ideal it's from biggerYieldpossible. Thus, it is not possible to have a thermal machine operating with the same temperatures as the sources hot and cold with yield greater than the yield of the Carnot cycle.
Machine performance based on the Carnot cycle can be calculated using the following formula:
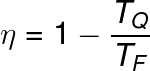
Subtitle:
TQ – hot source temperature (K)
TF– cold source temperature (K)
Lookalso: Carnot Machines
By Me. Rafael Helerbrock



