Imagine you want to push an object. The force you apply on it needs to be in the direction and direction in which you intend to move it or not will reach the desired result: if you want the object to go forward, of course it won't do any good to push it to low! That's because force is an example of vector magnitude. To describe it, it is also necessary to say the sense and direction in which it is applied.
There are other types of quantities that don't need all that description, for example, if someone asks for the time, you just have to say what time it is and the information has already been completely passed. These are the scalar quantities.
as the vector and scalar quantities are different, operations with them are also done in different ways. Vector quantities must be represented by vectors, which are straight lines with an arrow at the end that show the magnitude, direction and direction of the quantity. Look the following picture:

representation of a vector
The size of the line represents the magnitude (numerical value) of the vector, the line represents the direction of the quantity, and the arrow indicates the direction.
Mind Map: Vectors

*To download the mind map in PDF, Click here!
At vector operations they depend on the direction and direction between them. For each case, we use a different equation. See below the main operations that can be performed with vectors:
vectors in the same direction
To perform operations with vectors in the same direction, we must initially establish one direction as positive and the other as negative. We normally use as positive the vector that “points” to the right, while the negative is the vector that points to the left. After agreeing the signals, we add their modules algebraically:
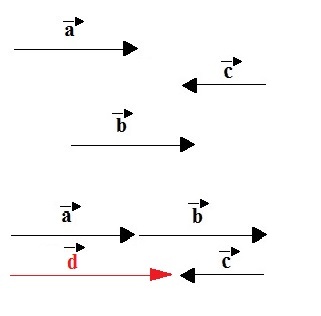
Vectors in the same direction and different directions
the vectors The, B and ç have the same direction, but the vector ç it has the opposite meaning. Using the sign convention, we have The and B with positive signs and ç with minus sign. Thus, the modulus of the resulting vector d will be given by the equation:
Do not stop now... There's more after the advertising ;)
d = a + b - c
the sign of d indicates the direction of the resulting vector: if d is positive, its direction will be to the right; but if it is negative, its direction will be to the left.
This is just one example of how to solve operations with vectors in the same direction, but the rule of signs is valid whenever there are vectors in these conditions.
vectors perpendicular to each other
Two vectors are perpendicular when they make a 90° angle to each other. Suppose a rover leaves point A and goes west, moving a distance d1 and arriving at point B. It then leaves point B and goes to point C, moving a distance d2now in the north direction, as shown in the figure:

Representation of vectors perpendicular to each other
The resulting detachment from point A to point C is represented by the vector d. Note that the figure formed corresponds to a right triangle, in which the vectors d1 and d2 we are hips and d is the hypotenuse. Therefore, we can calculate the modulus of d through Pythagorean theorem:
d2 = d12 + d22
Vectors in any directions
When two vectors make an angle α to each other, different from 90º, it is not possible to use the Pythagorean Theorem, but the operations can be done using the rule of parallelogram. The following figure shows the resulting displacement d of a piece of furniture that left point A and moved a distance d1 , arriving at point B; then he moved a distance d2 until you reach point C:

The resulting displacement d describes a parallelogram with d1 and d2
As the resulting displacement d forms a parallelogram with d1 and d2, it must be calculated with the equation:
d2 = d12 + d22 + 2d1d2 cosα
(Rule of parallelogram)
By Mariane Mendes
Graduated in Physics
*Mental Map by Me. Rafael Helerbrock
Would you like to reference this text in a school or academic work? Look:
TEIXEIRA, Mariane Mendes. "Operations with vectors"; Brazil School. Available in: https://brasilescola.uol.com.br/fisica/operacoes-com-vetores.htm. Accessed on June 27, 2021.

