Quadrilaterals they are polygons which have four sides. Polygons, in turn, are figures limited by straight segments. Thus, all sides of a polygon and, consequently, of a quadrilateral are straight.
Elements of a Quad
sides: They are the straight segments that skirt the quadrilateral;
vertices: These are the meeting points between two sides;
internal angles: Are the angles determined by two consecutive sides of a quadrilateral;
outside angles: are angles formed by the extension of one side of a polygon. An outside angle is always supplementary to the inside angle adjacent to it;
diagonals: Line segments whose endpoints are two non-consecutive vertices of a polygon. In this way, it is the line segments that connect two vertices and, at the same time, they are not sides.
General properties of quadrilaterals
The sum of the internal angles of a quadrilateral is always equal to 360°;
The sum of an inner angle of a quadrilateral and the outside angle adjacent to it equals 180°;
the perimeter of a quadrilateral is equal to the sum of the lengths of its sides.
Convex or non-convex quadrangles
Convex is the name given to a polygon which has the following characteristic: the line that contains one of its sides does not cut the polygon, whichever side is chosen to observe this line.
In other words, a convex polygon does not have vertices facing inwards, forming a kind of mouth. Look at the image with an example of non-convex quadrilateral, where the line containing one side cuts the polygon:

trapeze
trapeze they are quadrilaterals that have a pair of opposite and parallel sides. All characteristics and properties of quadrilaterals and the polygons are valid for the trapezoids. In addition to these, it is also possible that trapezoids have a specific characteristic, which also guarantees them a specific property.
Do not stop now... There's more after the advertising ;)
One trapeze is called isosceles when its two nonparallel (and opposite) sides are congruent. In this case, the specific property is: in isosceles trapezoids, the base angles are congruent.

parallelograms
You parallelograms they are the quadrilaterals which have two pairs of parallel sides. In addition to all the properties and characteristics of polygons, they also have the following specific properties:
Opposite sides are parallel and congruent;
Opposite angles are congruent;
Adjacent interior angles are supplementary;
The diagonals of a parallelogram meet at their midpoints.
You parallelograms they are commonly divided into four groups: any parallelograms, rectangles, diamonds, and squares. The first group is composed of parallelograms that do not belong to the other three.
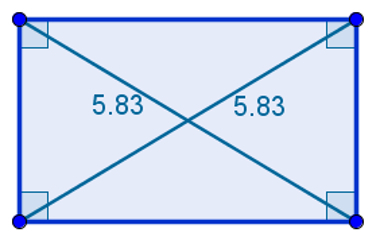
rectangles
They are parallelograms that have all right angles. Therefore, all its angles are equal to 90°. The specific property of rectangles is as follows:
“The diagonals of a rectangle are congruent.”
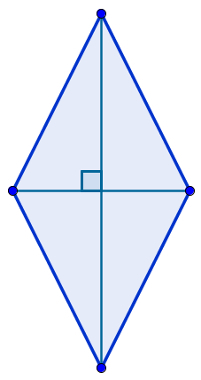
diamonds
They are parallelograms that have all four sides congruent. Note that diamonds need not have congruent angles, with the exception of opposite angles, of course. The specific property of diamonds is as follows:
“The diagonals of a diamond are perpendicular.”
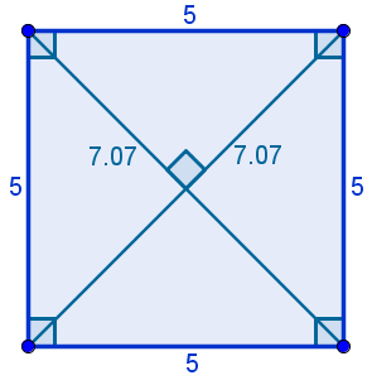
squares
You squares they are diamonds and rectangles at the same time, that is, they are parallelograms that have all congruent sides and all right angles. Therefore, we can say that every square is also a rectangle and rhombus, but not every rhombus or rectangle is square.
The specific property of squares it is the junction between the properties of the diamond and the rectangle. Watch:
“The diagonals of a square are perpendicular and congruent.”
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "What are quadrilaterals?"; Brazil School. Available in: https://brasilescola.uol.com.br/o-que-e/matematica/o-que-sao-quadrilateros.htm. Accessed on June 27, 2021.


