Half life, also known as semi-disintegration period, is the time it takes for half the number of atoms of the radioactive isotope present in a sample to disintegrate.
→ Disintegrations
THE disintegration it is not related to the extinction of the atom, that is, the atom does not cease to exist. In fact, what happens is the natural decay that the atom undergoes. At the decay, the atom (X), to the emit alpha radiation and beta, automatically transforms into a new chemical element (Y), which occurs incessantly until the atom ceases to be radioactive (stable atom).
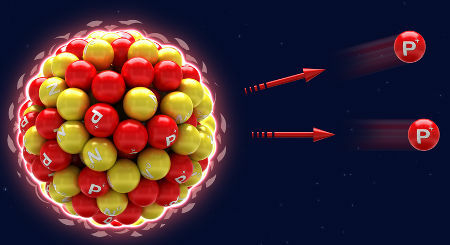
Representation of natural decay from alpha emissions (protons)
X → α + Y
Or
X → β + Y
If the Y atom formed in the decay is radioactive, new alpha and beta radiation will be emitted from that atom's nucleus. When you get to the half-life of a material, you know that half of the atoms that existed in the sample became stable.
→ Half-life of isotopes
Each radioactive isotope has a different half-life. This half-life can be expressed in seconds, minutes, hours, days and years. The table below shows the half-life of some radioactive isotopes:

Half-life values of some radioisotopes
→ Formulas used in the half-life study
The half-life period is represented by the acronym P. The time that a material has suffered disintegration is represented by t. Thus, if we know the half-life and the disintegration time (represented by x), we can say how many half-lives a material has had at a certain point in time. This is done through the list below:
t = x. P
With this knowledge, we can further determine the number of atoms that remain after the half-life period from the expression:
n = noO
2x
no = number of radioactive atoms remaining in the sample;
noO = number of radioactive atoms in the sample;
x = number of half-lives that have passed.
In addition to calculating the number of atoms itself, the disintegration or decrease in the amount of radioactive material after a half-life period can be expressed in the following ways:
→ As a percentage:
Pr = PO
2x
Pr= percentage of radioactive material remaining in the sample;
PO = initial percentage of radioactive material that was in the sample (always will be 100%);
x = number of half-lives that have passed.
→ In dough form:
m = mO
2x
m = mass of radioactive material remaining in the sample;
mO = mass of radioactive material in the sample;
-
x = number of half-lives that have passed.
Do not stop now... There's more after the advertising ;)
→ In the form of fractional numbers (fraction):
F = NO
2x
F = fraction referring to the radioactive material remaining in the sample;
NO= quantity referring to the radioactive material in the sample, which, in reality, is always number 1 in the case of exercises involving fractions;
x = number of half-lives that have passed.
→ Examples of calculations involving half-life
Follow now some examples of calculations that involve half-life:
Example 1: After 12 days, a radioactive substance has its activity reduced to 1/8 of its initial activity. What is the half-life of this substance?
Exercise Data:
Half-life (P) = ?
Total time (t) = 12 days
Remaining fraction (F) = 1/8
Initial quantity (NO) = 1
We have to determine the number of half-lives (x) suffered by the material in the following expression:
F = NO
2x
1 = 1
8 2x
2x.1 = 8.1
2x = 8
2x = 23
x = 3
We then determine the half-life value using the value of x found and the time provided by the utterance:
t = x. P
12 = 3.P
12 =P
3
P = 4 days
Example 2: A radioactive element has a half-life equal to 5 minutes. If you have 6 g of this element, what will its mass be after 20 minutes?
Exercise Data:
Half-life (P) = 5 minutes
Initial mass (mO) = 6 g
Total time = 20 minutes
Remaining mass (m) = ?
We initially determined the value of the amount of half-lives (x) that the material suffered through the time and half-life provided:
t = x. P
20 = x.5
20 = x
5
x = 4
Finally, we calculate the remaining mass through the value of x and the initial mass in the following expression:
m = mO
2x
m = 6
24
m = 6
16
m = 0.375 g
Example 3: A radioactive element has a half-life of 20 minutes. After how long will your mass reduce to 25% of the initial mass?
Exercise Data:
Half-life (P) = 20 minutes
Total time (t) = ?
Remaining percentage (Pr) = 25%
Initial percentage (PO) = 100%
We have to determine the number of half-lives (x) suffered by the material in the following expression:
Pr = PO
2x
25 = 100
2x
2x.25 = 100
2x = 100
25
2x = 4
2x = 22
x = 2
We then determine the value of time using the value of x found and the half-life provided by the statement:
t = x. P
t = 2.20
t = 40 minutes
By Me. Diogo Lopes Dias
Would you like to reference this text in a school or academic work? Look:
DAYS, Diogo Lopes. "What is half-life?"; Brazil School. Available in: https://brasilescola.uol.com.br/o-que-e/quimica/o-que-e-meia-vida.htm. Accessed on June 27, 2021.

