In the study of optics we saw that refraction is the name given to the phenomenon that occurs when light, when passing from one medium to another, undergoes a variation in its propagation speed. In the study of refraction we saw the two laws that govern this phenomenon. The first one says that the incident ray, the line N, normal to the separation surface at the point of incidence, and the refracted ray are coplanar, that is, they are in the same plane.
The second law of refraction, also known as the Snell-Descartes Law, says that, in refraction, the product of the refractive index of the middle (in which the radius is found by the sine of the angle that this radius forms with the straight line normal to the interface at the point of incidence) is constant. In this way, it is possible to write that:

It should be noted that when a light ray passes from one medium to another less refracting, the light ray refracts, moving away from the normal straight line perpendicular to the surface. Thus, it can be observed that, from a given angle of incidence, there is no longer refraction. This angle is called
limit angle or critical angle.Calculation of limit angle

According to the figure above, applying the Snell-Descartes Law to the situation allows us to calculate the sine of the limit angle L through the following relationship:
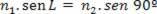
As sin 90º = 1, we have:
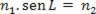
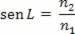
According to the above equation, we can see that the sine of the limit angle is the quotient between the refractive index of the least refracting medium by the refractive index of the most refracting medium, that is:

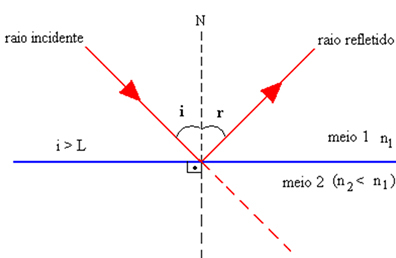
In the figure below we can see that when i > L, there is no refraction. Thus, the rays are all reflected and the phenomenon is called total internal reflection.
By Domitiano Marques
Graduated in Physics
Source: Brazil School - https://brasilescola.uol.com.br/fisica/calculo-angulo-limite.htm


