One 2nd degree equation is any equation with an unknown that is expressed as follows:
ax2 + bx + c = 0, a ≠ 0
The letter x is the unknown, and the letters a, b and ç are real numbers that function as the coefficients of the equation. just the coefficient The must be nonzero. If none of the coefficients is null, we say that it is a complete equation; but if any of the coefficients B and ç is zero, we say it is a incomplete equation.
When we solve a 2nd degree equation, we can find up to two results. These values are called roots of the equation. We'll see in this article how to determine the roots of a 2nd degree equation.
Whether the 2nd degree equation is complete or incomplete, we can use the Bhaskara formula to find your roots. Bhaskara's formula is as follows:
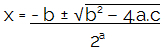
Just to simplify the notation, we commonly call the expression inside the square root of delta (?). calculating the ? separately, we can write Bhaskara's formula as follows:
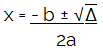
If the value of delta is less than zero, we say that the 2nd degree equation has no real roots. If delta equals zero, the equation will have two identical roots. If the delta is greater than zero, the 2nd degree equation will have two distinct roots.
Let's see an example of solving a 2nd degree equation using Bhaskara's formula.
x² + 3x + 2 = 0
The coefficients of this equation are: a = 1, b = 3 and c = 2. Let's first calculate the delta value:
? = b² - 4.a.c
? = 3² – 4.1.2
? = 9 – 8
? = 1
Now that we've found the value of delta, let's substitute it in Bhaskara's Formula to determine the roots of x:
x = – b ± √?
2nd
x = – 3 ± √1
2.1
x = – 3 ± 1
2
the sign of ± results in two roots of the equation. That way, first we'll find x', through the signal +, and then we'll find x'', through the sign of –:
x' = – 3 + 1
2
x' = – 2
2
x' = – 1
x'' = – 3 – 1
2
x'' = – 4
2
x'' = – 2
The roots of the equation x² + 3x + 2 = 0 they are – 1 and – 2.
If 2nd degree equation is incomplete, we can solve it without using Bhaskara's formula through the basic principles of solving equations.
By Amanda Gonçalves
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-equacao-2-grau.htm
