When we studied the ideal gas law, we saw that gases are composed of an immense amount of atoms and molecules. These molecules (or atoms) are in constant motion and their motion basically depends on the laws of kinematics. The characterization of the ideal gas law is given by the following equation:
PV = nRT
In this expression that we use to characterize an ideal gas, we use the amount of gas expressed in moles, that is, the mass divided by the molecular mass. In order to find the total mass of any gas, which corresponds to the number (n) of moles of molecules, we will multiply this number by the molar mass of the gas.
Let's look at a simple example: 1 mole of carbon atoms has a mass of 12 grams: the water molecule, composed of two atoms of hydrogen and one of oxygen, it has molecular mass M = (2 x 1) + 16 = 18 g/mol.
We can express the ideal gas law as a function of density. In this way, we can calculate the density variation of a gas when the pressure or temperature varies, without worrying about the volume. According to the gas law equation above, we can rewrite it as follows:

In the equation above, we note that n/V is the number of moles of atoms or molecules per unit volume. Thus, to find the density, we simply multiply n/V by the molecular mass M of the gas in question. Therefore, multiplying both sides of the equation by the molar mass of the gas, we get:
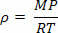
Which says that the absolute density of a gas is directly proportional to molecular mass and pressure is inversely proportional to temperature.
Remember if:
1 mol = 6.02 x 1023 molecules
Molecular mass is the mass of 1 mole of molecules
1 mole of gas in CNTP* (0ºC 1atm) occupies 22.4 liters.
*CNTP - normal temperature and pressure conditions
By Domitiano Marques
Graduated in Physics
Brazil School Team
Source: Brazil School - https://brasilescola.uol.com.br/fisica/a-densidade-lei-dos-gases-ideais.htm

