THE triangle classification is very useful for the development of the study and the specific properties of this geometric figure, which has great importance in plane geometry. They exist two ways to classify triangles. One of them takes into account the angles and in that case a triangle can be acute, when it has all its internal acute angles; rectangle, when one of its internal angles is straight; or obtuse angle, when one of its internal angles is obtuse.
The other classification is based on the comparison between the sides. In this case, a triangle can be scalene, when all sides have different measurements; isosceles, when there are two sides that have the same measure; or equilateral, when all sides are congruent.
Read too: Parallelogram - polygon that has parallel opposite sides
Triangle properties

a triangle is apolygon three sided, three vertices and three angles. Usually the vertices are represented by capital letters of our alphabet, and the measure of the sides is represented by small letters. Angles are represented by letters from the Greek alphabet.
There are elements and properties common to all triangles, that are:
- The triangle has no diagonal.
- The triangle has three external angles whose sum is always equal to 360º.
- The sum of the internal angles (Si) is always equal to 180º.
- The sum of any two sides is always less than the third side.
- Every triangle has height, median, bisector and bisector.
- Every triangle has important notable points: barycenter (meeting the three medians), circumcenter (meeting of the three bisectors), incentro (meeting of the three bisectors) and orthocenter (meeting of the three heights).
- THE area of a triangle any can be calculated by the formula:

THE: area
B: base
H: height
Triangle classification
There are two ways to classify triangles, which are independent of each other. One of them takes into account angles – in this case, a triangle can be obtuse-angled, acute-angled or rectangle. The other way of classifying, on the other hand, compares the length of each side, so a triangle can be scalene, equilateral or isosceles.
Classification of triangles by angles
By analyzing the internal angles of the triangle, we arrive at three cases:
Acute Triangle
A triangle is known as an acute-angle when its three angles are acute, that is, less than 90º.

rectangle triangle
A triangle is a rectangle when one of your angles is straight, that is, equal to 90º. As the sum of the three angles is always equal to 180°, the other angles are necessarily acute.

The right triangle is very important for Mathematics, because, based on it, relationships of great importance are developed, such as the trigonometric relations in the right triangle it's the Pythagorean theorem. To learn more about this type of triangle, visit our text: right triangle.
obtuse triangle
A triangle is obtuse when one of your angles it's obtuse, that is, greater than 90º. The other angles are necessarily acute.

See too: Similarity of triangles - comparison between proportional sides and congruent angles
Ranking on the side
Analyzing the sides of the triangle, we can also separate three cases:
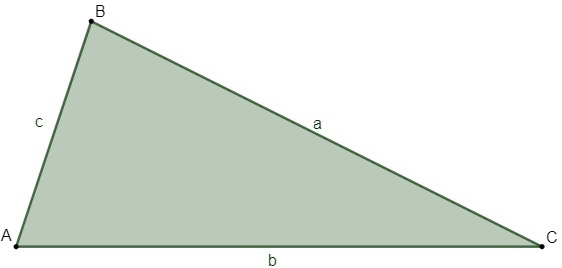
scalene triangle
The triangle is scalene when the side measurements are all different.
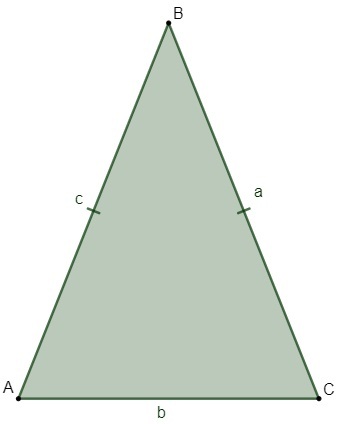
isosceles triangle
the triangle is isosceles when you have at least two congruent sides, that is, with the same measure. Due to this particularity, the isosceles triangle has specific properties, which are not valid for scalene triangles.
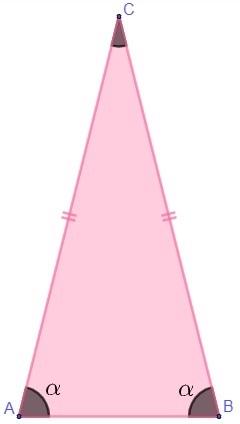
At specific properties of the isosceles triangle are two, one in relation to angle and one in relation to height.
In isosceles triangles, the base angles are always equal (we treat as base the side that has a different measurement from the other sides).
When plotting the height H of the isosceles triangle, it divides the base into two equal parts.

Note that the segments AM and BM are congruent, meaning that M is the midpoint of the base of this triangle.
Equilateral triangle
the triangle is equilateral when you have thes three sides with the same measurements. As a result, the three angles also have the same measurement, which is 60°. There are specific formulas for calculating the area and height of this triangle, which are deduced from the three congruent sides.

In the equilateral triangle, the properties of the isosceles triangle are also valid, after all, it has more than two equal sides. Furthermore, knowing the side of the equilateral triangle, we can find the height and its area using the following formulas:
height of equilateral triangle
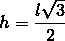
equilateral triangle area

Also access: Trapezium - four-sided polygon with two parallel
solved exercises
Question 1 - From the sentences below, tick the one that is true.
A) An equilateral triangle can be a rectangle.
B) Every right triangle is scalene.
C) Every equilateral triangle is acute.
D) Every obtuse triangle is isosceles.
E) Every isosceles triangle is acute-angled.
Resolution
Alternative C.
Analyzing the alternatives, we have to:
A) An equilateral triangle has all sides equal and, consequently, all angles, which measure 60º, which makes it impossible for an equilateral triangle to be right.
B) By the argument of the previous alternative, we know that a right triangle cannot be equilateral, it remains to be seen whether it can be isosceles. Knowing that it has an angle of 90º, if the other two angles are 45º each, we have an isosceles right triangle, so not every right triangle is scalene.
C) Knowing that the internal angles of an equilateral triangle are 60°, then it is true that it is acute.
D) An obtuse triangle can be isosceles (for example, if its angles measure 100º, 40º and 40º) and scalene as well (for example, if it has angles of 120º, 20º and 40º). There are several other possibilities for it to be scalene, which makes the statement false.
E) From the explanation of the letter D, we know that an isosceles triangle can be obtuse, and from the explanation of the letter B, we know that it can be rectangle, which makes this sentence false.
Question 2 - Check the correct alternative on the classification of triangles.
A) Equilateral triangle is one that has all angles measuring 90º.
B) Isosceles triangle is one that has all different sides.
C) Acute-angle triangle is one that has exactly one acute angle.
D) Obtuse triangle is one that has an obtuse angle.
E) Right triangle is one that has all of its right angles.
Resolution
Alternative D.
a) The equilateral triangle has all angles equal to 60º, not 90º.
b) The isosceles triangle is one that has at least two equal sides.
c) The acute-angled triangle has all the acute angles, not just one.
d) This alternative is the true one, as this is the definition of an obtuse-angled triangle.
e) The right triangle has only one right angle.
Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/classificacao-de-triangulos.htm