O uniformly varied circular motion, or simply MCUV, is an accelerated motion in which a particle moves along a circular path of constant radius. Unlike the uniform circular movement, in the MCUV, there is, in addition to the centripetal acceleration, one angular acceleration, responsible for a variation in the speed at which the angle is traversed.
Uniformly varied circular motion can be understood more easily if we know the hourly equations of MUV, since the MCUV equations are similar to them, but are applied to angular quantities.
See too: Uniform circular motion (MCU) — concepts, formulas, exercises
MCU and MCUV
MCU and MCUV they are circular movements, however, in the MCU, the angular velocity is constant and there is no angular acceleration. In the MCUV, the angular velocity is variable, due to a constant angular acceleration. Despite being called a uniform circular motion, the MCU is an accelerated motion since in both there is a centripetal acceleration, which causes a particle to develop a circular path.

MCUV theory
As we said, the MCUV is one in which a particle develops a circular trajectory of lightningconstant. In addition to centripetal acceleration, responsible for constantly changing the direction of the particle's tangential velocity, there is also a accelerationangular, measured in rad/s². This acceleration measures the variationgivesvelocityangular and, as it is a uniformly varied movement, it has a constant modulus.
The MCUV equations are similar to the Uniformly Varied Motion (MUV) equations, however, instead of using the hourly equations of position and velocity, we use the MCUV equations. equationshoursangles.
See too: Mechanics - types of movement, formulas and exercises
Do not stop now... There's more after the advertising ;)
MCUV formulas
MCUV formulas are easy to understand if you already understand uniformly varied motion. For each of the MUV formulas, there is a corresponding one in the MCUV. Watch:
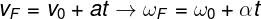
vF and you0 – final and initial speeds (m/s)
ωF and ω0 – final and initial angular velocities (rad/s)
The – acceleration (m/s²)
α – angular acceleration (rad/s²)
t – instant of time(s)
Above we show the hourly velocity functions, respectively, related to MUV and MCUV. Next, we look at the hourly function of the position for each of these cases.

sF and S0– end and start positions (m)
ΘF and Θ0 – final and initial angular position (rad)
In addition to the two fundamental equations shown above, there is also the Torricelli equation for the MCUV. Look:

S – spatial displacement (m)
ΔΘ – angular displacement (rad)
There is also a formula that is used to explicitly calculate the angular acceleration of motion, namely:
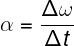
Now that we know the main MCUV formulas, we need to do some exercises. Come on?
Lookalso: Seven "golden" tips to study Physics on your own and do well on exams!
Solved exercises on the MCUV
Question 1 — A particle moves along a circular path with a radius equal to 2.5 m. Knowing that, at t = 0 s, the angular velocity of this particle was 3 rad/s and that, at time t = 3.0 s, its angular velocity was equal to 9 rad/s, the angular acceleration of this particle, in rad/s², is equal The:
a) 2.0 rad/s².
b) 4.0 rad/s².
c) 0.5 rad/s².
d) 3.0 rad/s².
Resolution:
Let's calculate the angular acceleration of this particle. Note the calculation below:

Based on the calculation, we find that the angular acceleration of this particle is 2 rad/s², so the correct alternative is letter a.
Question 2 — A particle develops an MCUV from rest, accelerating at a rate of 2.0 rad/s². Determine the angular velocity of this particle at the instant of time t = 7.0 s.
a) 7.0 rad/s
b) 14.0 rad/s
c) 3.5 rad/s
d) 0.5 rad/s
Resolution:
To answer this question, let's use the hourly speed function on the MCU. Watch:

According to our calculation, the angular velocity of the particle at time t = 7.0 s is equal to 14.0 rad/s, so the correct alternative is letter B.
By Rafael Hellerbrock
Physics teacher



