THE magnetic force it is the result of the interaction between two bodies endowed with magnetic properties, such as magnets or electrical charges in motion. she can be so much attractive how much repulsive and appears in bodies electrically charged and that they are in motion relative to some external magnetic field. This force is always perpendicular to the velocity vectors of the body and the magnetic field.
magnetic force on charged particles
For bodies of negligible dimensions, we use the following equation to calculate the magnetic force:
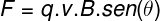
For this force to be measured in Newtons (N), the module of charge liquid (q) of the body, that is, the charge in excess or lack, must be given in Coulombs; The velocity of the particle (v) in relation to the magnetic field must be given in m/s; O angle(θ) formed between the speed (v) and the magnetic field (B), in Tesla (T), must be given in degrees (º). Look at the figure to better understand this relationship:
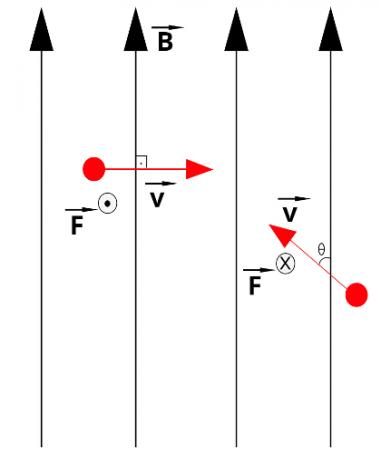
In the figure above, we have two charged particles
(in red) moving with speed v in a region where the magnetic field is constant and vertical for up. The direction of the magnetic force depends on the right hand rule. Also, if she is "going out” of the paper plane, we use a circle with a dot in the center; if she is "entering” on the paper plane, we use a circle with a “X" in the center.The following figure teaches you how to use the right hand rule to determine the direction of the magnetic force:
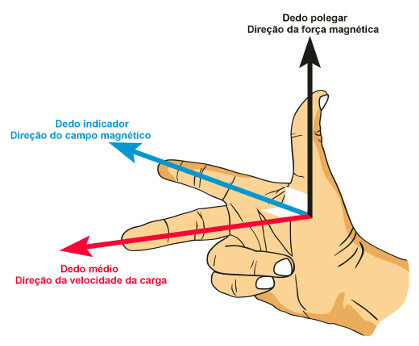
point the index finger in the direction of the magnetic field. the middle finger must point in the direction gives velocity of the particle, and the thumb must point the direction and direction of the magnetic force. It is important to note that these three quantities will always be perpendicular, so if the angle formed between the velocity vector (v) and the magnetic field vector (B) is equal to 0º, that is, if they are parallel to each other, there will be no appearance of magnetic force; likewise, the greatest intensity of magnetic force arises when the angle between v and B it's from 90º, because, for this angle, the sin (θ) has its value maximum, worth 1.
Do not stop now... There's more after the advertising ;)
If the charge on the particle is negative, just reverse the direction of the thumb. Use the rule in the same way and, at the end, reverse it: if the thumb points up, the magnetic force points down and vice versa.
Magnetic force on straight conductors
If a straight conductor wire, such as a wire, is being traversed by an electric current in a region where there is an external magnetic field, it will suffer the action of a magnetic force. We can calculate the intensity of this magnetic force using the following equation:
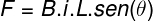
B is the value of the magnetic field strength in Tesla (T);
i is the value of the electric current in Amperes (THE);
L is the length of the wire in meters (m).
The angle, in this case, is formed between the magnetic field and the length of the wire, so it must be straight; otherwise, we would have to calculate the magnetic force on each piece of wire that has a different angle. In the figure below, we have a wire covered by an electrical current (i) in a region of magnetic field (pointing away from the plane of the paper). Note the direction of the magnetic force in each part of the wire:

Now that you know what magnetic force is, pay attention to the details:
The magnetic force is always perpendicular (90º) at the speed of the charged particle and the magnetic field, simultaneously;
How the magnetic force makes a 90° angle with the particle's velocity, the velocity does not change, only its direction and direction, so the magnetic force does not do work;
If the angle between the velocity (θ) it's the magnetic field is from 0º, there will be no magnetic force.
By Rafael Hellerbrock
Graduated in Physics
Would you like to reference this text in a school or academic work? Look:
HELERBROCK, Rafael. "What is magnetic force?"; Brazil School. Available in: https://brasilescola.uol.com.br/o-que-e/fisica/o-que-e-forca-magnetica.htm. Accessed on June 27, 2021.
