Kepler's Laws on planetary motion were developed between 1609 and 1619 by the German astronomer and mathematician Johannes Kepler. Kepler's three laws, used to describe the orbits of the planets of Solar system, were built on the basis of precise astronomical measurements, obtained by the Danish astronomer. Tycho Brahe.
Introduction to Kepler's Laws
Contributions left by Nicolas Copernicus in the area of astronomy broke with the vision geocentrist of the Universe, derived from the planetary model of Claudio Ptolemy. The model suggested by Copernicus, although complex, allowed the prediction and the explanation of the orbits of several planets, however, it had some flaws, the most dramatic of which being a satisfactory explanation for the retrograde orbit of Mars during certain periods of the year.
See too:history of astronomy
The resolution of inexplicable problems by Copernicus' planetary model came only in the 17th century, by the hands of Johannes Kepler. To that end, Kepler admitted that the planetary orbits were not perfectly circular, but rather
elliptical. In possession of extremely accurate astronomical data, carried out by Brahe, Kepler established two laws that govern the movement of planets, 10 years later, he published a third law, which allows to estimate the orbital period or even the orbit radius of the planets that revolve around of Sun.
Kepler's Laws
Kepler's laws of planetary motion are known as: law of elliptical orbits,law of areas and law of periods. Together these explain how the movement of any body orbiting a massive star works, such as planets or stars. Let's check what is stated in Kepler's laws:
1st law of Kepler: law of orbits
THE Kepler's first law states that the orbit of planets revolving around the sun is not circular but elliptical. Furthermore, the Sun always occupies one of the focuses of this ellipse. Although elliptical, some orbits, like Earth's, are very close to a circle, as they are ellipses that have a eccentricitymuchlittle. Eccentricity, in turn, is the measure that shows how much a geometric figure differs from a circle and it can be calculated by the relationship between the semi-axes of the ellipse.
"The orbit of the planets is an ellipse in which the Sun occupies one of the focuses."
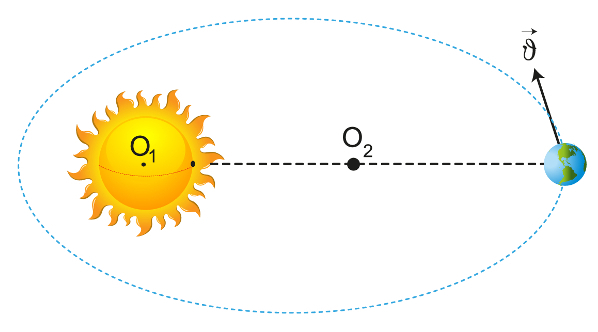
2nd law of Kepler: law of areas
Kepler's second law states that the imaginary line connecting the Sun to the planets orbiting it sweeps areas at equal time intervals. In other words, this law states that the the speed with which the areas are swept is the same, that is, the halo velocity of the orbits is constant.
"The imaginary line connecting the Sun to the planets orbiting it sweeps across equal areas at equal time intervals."

Kepler's 3rd law: law of periods or law of harmony
Kepler's third law states that the square of a planet's orbital period (T²) is directly proportional to the cube of its average distance from the Sun (R³). Furthermore, the ratio between T² and R³ has exactly the same magnitude for all the stars that orbit this star.
"The ratio between the square of the period and the cube of the average radius of a planet's orbit is constant."
The expression used to calculate Kepler's third law is shown below, check it out:

T – orbital period
R – average radius of the orbit
Look at the next figure, in it we show the major and minor axes of a planetary orbit around the Sun:
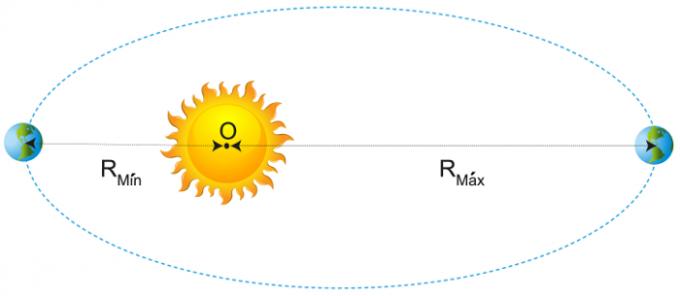
The average radius of the orbit, used in the calculation of Kepler's third law, is given by the average between the maximum and minimum radii. The positions shown in the figure, which characterize the Earth's greatest and shortest distance from the Sun, are called aphelion and perihelion, respectively.
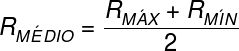
When the Earth approaches the perihelion, your orbital speed increases, since the gravitational acceleration of the Sun intensifies. In this way, the Earth has maximum kinetic energy when near the perihelion. Approaching aphelion, it loses kinetic energy, thus having its orbital velocity reduced to its smallest measure.
Know more: Gravitational acceleration - formulas and exercises
The more detailed formula of Kepler's third law is shown below. Note that the ratio between T² and R³ is determined exclusively by two constants, the number pi and the constant of universal gravitation, and also by the pasta of the sun:

G – constant of universal gravitation (6.67.10-11 N.m²/kg²)
M – mass of the Sun (1,989.1030 kg)
This law was not obtained by Kepler, but by Isaac Newton, through law of universal gravitation. To do it, Newton identified that the gravitational force of attraction between the Earth and the Sun is a centripetal force. Observe the following calculation, it shows how it is possible to obtain, based on the law of universal gravitation, the general expression of Kepler's third law:

Also know:What is centripetal acceleration?
Check the table below, in which we show how the measurements of T² and R³ vary, in addition to their ratio, for each of the planets in the Solar System:
Planet |
Mean radius of orbit (R) in AU |
Period in terrestrial years (T) |
T²/R³ |
Mercury |
0,387 |
0,241 |
1,002 |
Venus |
0,723 |
0,615 |
1,001 |
Earth |
1,00 |
1,00 |
1,000 |
Mars |
1,524 |
1,881 |
1,000 |
Jupiter |
5,203 |
11,860 |
0,999 |
Saturn |
9,539 |
29,460 |
1,000 |
Uranus |
19,190 |
84,010 |
0,999 |
Neptune |
30,060 |
164,800 |
1,000 |
The average radius of the orbits in the table is measured in astronomical units (u). An astronomical unit corresponds to distanceaverage between the Earth and the Sun, about 1,496.1011 m. In addition, the small variations in the T² over R³ ratios are due to precision limitations in the measurements of the orbital radius and the period of translation of each planet.
Lookalso: Centripetal force applications - spines and depressions
Exercises on Kepler's Laws
Question 1) (Ita 2019) A space station, Kepler, studies an exoplanet whose natural satellite has an elliptical orbit of semi-major a0 and period T0, where d = 32a0 the distance between the station and the exoplanet. An object that detaches from Kepler is gravitationally attracted to the exoplanet and starts a free fall movement from rest in relation to it. Neglecting the exoplanet's rotation, the gravitational interaction between the satellite and the object, as well as the dimensions of all the bodies involved, calculate as a function of T0 the falling time of the object.
Template: t = 32T0
Resolution:
If we take into account that the eccentricity of the elliptical trajectory that the object will describe is approximately equal to 1, we can assume that the object's orbit radius will be equal to half the distance between the Kepler space station and the planet. In this way, we will calculate how long the object should approach the planet from its initial position. For that, we must find the period of the orbit, and the fall time, in turn, will be equal to half of that time:
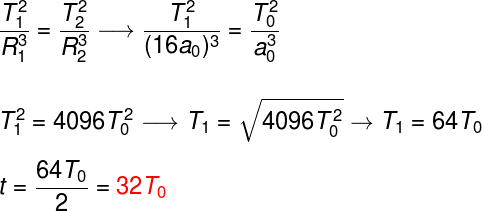
After we have applied Kepler's third law, we divide the result by 2, since what we calculate was the orbital period, in which, in half the time, the object falls towards the planet, and in the other half, moves away. Thus, the fall time, in terms of T0, it's the same as 32T0.
Question 2) (Udesc 2018) Analyze the propositions regarding Kepler's laws on planetary motion.
I. The speed of a planet is greatest at perihelion.
II. Planets move in circular orbits, with the Sun at the center of the orbit.
III. A planet's orbital period increases with the average radius of its orbit.
IV. The planets move in elliptical orbits, with the Sun at one of the focuses.
V. The speed of a planet is higher in aphelion.
tick the alternative correct.
a) Only statements I, II and III are true.
b) Only statements II, III and V are true.
c) Only statements I, III and IV are true.
d) Only statements III, IV and V are true.
e) Only statements I, III and V are true.
Template: Letter C
Resolution:
Let's look at the alternatives:
I - REAL. When the planet approaches perihelion, its translational speed increases, due to the gain in kinetic energy.
II - FALSE. Planetary orbits are elliptical, with the Sun occupying one of their focuses.
III - REAL. The orbital period is proportional to the radius of the orbit.
IV - REAL. This assertion is confirmed by the statement of Kepler's first law.
V - FALSE. The speed of a planet is greatest near perihelion.
Question 3) (Phew) Many theories about the Solar System followed, until, in the 16th century, the Polish Nicolaus Copernicus presented a revolutionary version. For Copernicus, the Sun, not the Earth, was the center of the System. Currently, the accepted model for the Solar System is basically that of Copernicus, with corrections proposed by the German Johannes Kepler and subsequent scientists.
On gravitation and Kepler's laws, consider the following statements, true (I will fake (F).
I. Adopting the Sun as a reference, all planets move in elliptical orbits, with the Sun as one of the focuses of the ellipse.
II. The position vector of the center of mass of a planet in the Solar System, in relation to the center of mass of the Sun, sweeps equal areas at equal time intervals, no matter the planet's position in your orbit.
III. The position vector of the center of mass of a planet in the Solar System, relative to the center of mass of the Sun, sweeps proportional areas at equal time intervals, regardless of the planet's position in its orbit.
IV. For any planet in the Solar System, the quotient of the cube of the average radius of the orbit and the square of the period of revolution around the Sun is constant.
tick the alternative CORRECT.
a) All statements are true.
b) Only statements I, II and III are true.
c) Only statements I, II and IV are true.
d) Only statements II, III and IV are true.
e) Only statements I and II are true.
Template: Letter C
Resolution:
I. TRUE. The statement is the very statement of Kepler's first law.
II. TRUE. The statement coincides with the definition of Kepler's second law.
III. FALSE. The determination of Kepler's second law, which follows from the principle of conservation of angular momentum, implies that the swept areas are equal for equal time intervals.
IV. TRUE. The statement reproduces Kepler's third law statement, also known as the law of periods.
By Me. Rafael Helerbrock
