Work of a force: what is it, calculation, exercises

Work is the transfer of energy to a body or system of bodies due to the application of a force. The work that is done on a body produces a kinetic energy variation.

Through this important magnitude of dynamics, it is possible to study the transfer and transformation of energy in the most diverse physical systems.

Read too: What is strength?

What is work?

work is a physical quantity which measures the transfer or transformation of energy. The unit of measure of this scalar quantity is the joule. Furthermore, the work that is performed by a force is equivalent to the variation of kinetic energy, as well as the potential energy attributed to a body or system of bodies.

When work is done on a body, some of the energy that was stored in that body is transformed into other forms of energy. When we raise an object from the ground to a height h, for example, we are transforming an energy that is from our muscles to this body, which, after being elevated, starts to present a certain amount in andgravitational potential energy.

instagram story viewer

When we lift a body, we are doing work on it.

It is noteworthy that the work is calculated based on the distance traveled by the body. However, for this calculation, only the distance traveled in the direction of the force performing the work is taken into account — in other words, work is equal to vector projection strength about the direction of the distance traveled by the body.

How is the work of a force calculated?

To calculate the work performed by a constant force, it is necessary to multiply the module of this force by the distance traveled and by cosine of angle which is formed between force (F) and distance (d). The formula we use to calculate the work is as follows:

From the displayed formula, you can see that there is no work performed when the angle between force and distance is equal to 90º, since the cosine of this angle is equal to zero. This is because when a force is applied in a direction perpendicular to a displacement, this force does not promote any variation in the kinetic energy of the body, but only changes the direction of its movement.

Motor work and tough work

motor work is the name given to the work that is carried out to favor of the movement of a body, providing him with kinetic energy. On the other hand, the workresistant is the one where a strengthcontraryto themovement, causing the body to have its kinetic energy reduced and/or transformed into other types of energy, such as gravitational potential energy or Thermal energy, in the case where a dissipative force.

In motor work, the force and displacement vectors are parallel (0° angle). In resistant work, these vectors are opposite (180º angle). Check out examples of situations in which motor work and resistant work are performed.

When we push a shopping cart, we perform motor work.
When a bicycle's brake pads press on the rim, the frictional force does a tough job.
When we are descending a ladder, the force of weight performs motor work.
When we climb a ladder, the weight force does a tough job.

Read too: Traction - force exerted on a body through ropes, cables or wires

strength work weight

The work performed by the weight force corresponds to the amount of energy needed to raise a body of mass m to a height h in relation to the ground, in a region where the gravity worth g. See the formula used to calculate the work of the strength weight:

m – body mass (kg)

g – gravity (m/s²)

H – height (m)

Electric power work

The calculation of electric power work can be made from the product between the load modulus and the difference of electric potential, in volts, to which this load is subjected.

τ – work (J)

what – electric charge (C)

U – potential difference (V)

Work of a variable strength

The work of a variable force can be calculated from a graph that relates the force to the displacement suffered by the body. In this case, the modulus of the work performed is numerically equal to area under the curve. Watch:

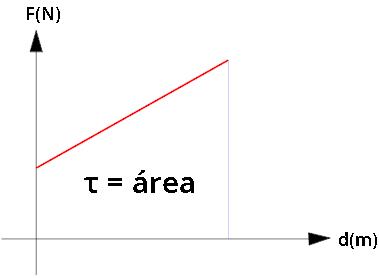
The Fxd graph area represents the module of work performed.

Work and kinetic energy theorem

The work and kinetic energy theorem relates the amount of work that is done on a body or on a system of bodies according to the variation of its kinetic energy. In other words, every work performance is accompanied by a variation of kinetic energy.

In short, we say that the work performed is equal to the variation in kinetic energy:

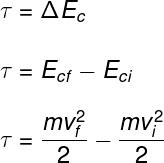
The theorem above states that work is equivalent to the variation of kinetic energy.

To learn even more about the definition of work, it is necessary to solve some exercises on the subject. Come on?

See too: How to Solve Newton's Law Exercises

Solved exercises on the work of a force

Question 1 — (Espcex) A block, pulled by means of an inextensible rope and negligible mass, slides over a horizontal surface with friction, describing a straight and uniform movement. The rope makes an angle of 53° with the horizontal and the traction it transmits to the block is 80 N. If the block is displaced 20 m along the surface, the work performed by traction on the block will be:

(Data: sin 53° = 0.8 and cos 53° = 0.6)

a) 480 J

b) 640 J

c) 960 J

d) 1280 J

e) 1600 J

Resolution:

To answer this question, it is necessary to use the formula of the work, but also to identify the pertinent data in the statement, which are the force, distance and cosine of the angle. Then you need to do the following calculation:

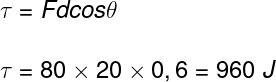
Based on the result obtained, we conclude that the correct alternative is the letter C.

Question 2 — (CPS) To transport fertilized land removed from the compost, a farmer fills a wheelbarrow and takes it to the planting site by applying a horizontal, constant force with an intensity equal to 200 N. If during this transport, the resulting force applied was able to do 1800 J work, then the distance between the compost heap and the planting site was, in meters:

a) 6

b) 9

c) 12

d) 16

e) 18

Resolution:

The question asks us to calculate the distance and, for that, we are informed the module of the amount of work, as well as the force. In this way, we must make the following calculation:

According to the calculation, the correct alternative is the letter B.

Question 3 — (Mackenzie) At the Rio 2016 Olympics, our pole vault gold medalist, Thiago Braz, weighing 75.0 kg, reached a height of 6.03 m, a world record, falling 2.80 m from the pole's support point. Considering the gravity acceleration module g = 10 m/s², the work performed by the weight force during the descent was approximately:

a) 2.10 kJ

b) 2.84 kJ

c) 4.52 kJ

d) 4.97 kJ

e) 5.10 kJ

Resolution:

The answer to this question requires us to calculate an amount of work. To do this, we need to know the values of mass, gravity and height. In possession of these values, just do the calculation: