When studying some physical concepts, we should not forget that many of the concepts need to be characterized and for this we make use of measurement units. But there are some concepts that need more features, such as vectors. Quantities that need to be characterized by a modulus (number followed by a unit) and a spatial orientation are called vector quantities.
In the study of vector acceleration we saw that it can vary in module and direction. Therefore, to facilitate its analysis, the vector acceleration at a given point of a trajectory is decomposed in two component accelerations: a so-called tangential acceleration, related to the variation of the modulus of the vector velocity; and another, normal to the trajectory, called centripetal acceleration, which is related to the variation in the direction of the velocity vector.
Tangential Acceleration Component Characteristics
- tangential acceleration measures how quickly the magnitude of the velocity vector varies;
- it has a modulus equal to the scalar acceleration modulus;
- its direction is always tangent to its trajectory;
- the direction is the same direction adopted for the velocity vector if the movement is accelerated; if the movement is delayed, the direction is opposite to the velocity vector;
- the magnitude of the tangential acceleration vector is null in uniform motions.
Centripetal Acceleration Component Characteristics
Do not stop now... There's more after the advertising ;)
- the centripetal component measures how quickly the direction of the velocity vector varies;
- has radial direction and always points to the center of the trajectory;
- has module given by Thecp = v2/R, where v is the instantaneous velocity and R is the radius of the trajectory described by the rover;
- in rectilinear movements, the direction of the velocity vector does not change, so the centripetal acceleration is null.
How to determine the acceleration vector?
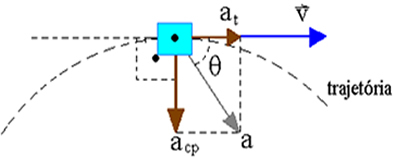
We know that the tangential acceleration vector is tangent to the trajectory. It is oriented in the same direction as the movement and its magnitude is equal to the value of the scalar acceleration.
From the figure above we can determine the centripetal acceleration vector. According to the figure, we can see that it is normal to the trajectory, it is oriented to the center of the trajectory and its magnitude is given by the following equation:
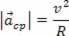
Still in relation to the figure above, we see that the tangential and centripetal components are orthogonal. Therefore, we can make use of the Pythagorean Theorem to write:

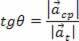
By Domitiano Marques
Graduated in Physics
Would you like to reference this text in a school or academic work? Look:
SILVA, Domitiano Correa Marques da. "Vector acceleration characteristics"; Brazil School. Available in: https://brasilescola.uol.com.br/fisica/caracteristicas-aceleracao-vetorial.htm. Accessed on June 27, 2021.


