There is no point in learning different mathematical concepts without having an understanding of the application of these concepts, even in hypothetical situations. For now we will see the application of two trigonometric laws that apply in any situation where you have a triangle, whatever it is.
The concepts are those of the sine and cosine laws, concepts that work with only two elements: angle and side measurement.
We will see the same situation, where a bridge builder wants to calculate the size of the bridge that will be built, however, in each situation the information will be different. With this, we will see the cases in which it is possible to apply the Sine Law and the Cosine Law.
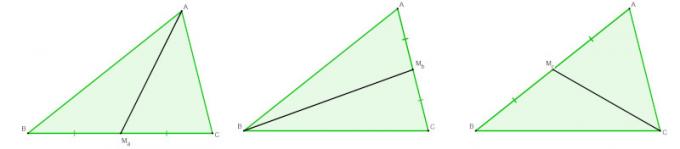
Situation 1) The builder wants to calculate the distance from point A to point C, points where the bridge will be built, however he doesn't have any tool that measures this distance, but he knows math and had the following idea. "As I have a tool that calculates angles, I will be able to determine the length of this bridge." With this he marked a point B, calculated the angle BÂC which was equal to 85°, walked to point B, a distance of 2km, and calculated the angle ABC obtaining an angle of 65°. The builder believes that with this information it will be possible to calculate the length of the bridge.
See how this calculation will be performed:

Note that the only information given was:
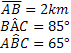
Let's see the expressions of the Trigonometric Laws that can be applied.
Sine law:
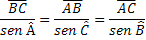
Cosine law:

See that with the data we have it is not possible to apply the cosine law, as we need the measurements from two sides and we only have the measure of one side and two angles, so we will apply the law of sines.
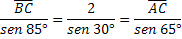
The objective is to determine the value of the AC segment, so we will use the last two proportions.
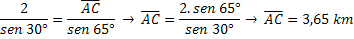
Situation 2) The builder wants to calculate the distance from point A to point C, points where the bridge will be built, however, with the tool that it has, it was only possible to calculate the measurements of segments AB and BC, in which segment AB is equal to 2km and segment BC 3.99km. He used the angle measuring tool again and found that the angle of vertex B is equal to 65°. With this, the builder was able to determine the length of the bridge. Do these calculations yourself.
Let's look at the information we have:
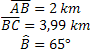
We have the measurement of two sides and only one angle. An important fact that allows us to apply the law of cosines is that the angle informed is determined by the two sides that are known.

Thus, we must pay attention to the information that the situation gives us, so that we know which relationship we should use. This is the crucial point to differentiate these two laws regarding their application.
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Source: Brazil School - https://brasilescola.uol.com.br/matematica/aplicacoes-das-leis-trigonometricas-um-triangulo-seno-.htm