You resistors are devices that can transform the energyelectric in heat through the joule effect. When electrons pass through resistors, the resulting particles collide with the crystal lattice of the material that makes up the resistor cause an increase in its thermal agitation, resulting in heat transfers to the vicinity of the resistor.
For this reason, resistors are widely used in circuits that are intended to produce heat, such as in electric heaters, electric cookers, electric fryers, irons, electric showers etc.

Resistors come in different colors and shapes.
This ability of resistors to produce thermal energy is directly related to their electrical resistance. Electrical resistance is the magnitude that measures the difficulty of establishing a electric current through different bodies.
This property depends on the shape of the body, the amount of free electrons present in the material and the time and distance that these electrons are able to be conducted without colliding with the atoms that make up the body, between others. The greater the resistance of a resistor, the greater the amount of energy it dissipates as heat each second, in other words, the greater the
potency by him dissipated.See too:Ohm's second law

Incandescent light bulbs have a high electrical resistance filament that heats up and emits light with the passage of electrical current.
The physical quantity that measures the amount of heat that a resistor transfers to its surroundings every second is called the potencydissipated. The dissipated power is a scalar quantity measured in Watts (W).
In physics, the power quantity has a very broad meaning, but its definition is always relative to reason between one the amountinenergy (E) and a certain breakintime (Δt).
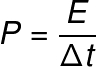
P – power (W)
AND – Energy (J)
t – time interval(s)
Therefore, the power that is dissipated by a resistor is a measure of how much energy that resistor is capable of transforming into heat each second.
The energy that is daily called electrical energy, in turn, is called energypotentialelectric. Its modulus can be calculated by the product between the electrical potential (U), given in Volts (V), and the modulus of a test load (q), inserted in this electrical potential:
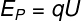
ANDP– Electric potential energy (J)
what – Test load (C)
U – Electric potential (V)
If we substitute the expression above in the definition of power, we have the following relationship:

PD – Power dissipated (W)
what – test electrical charge (C)
i – electric current (A)
According to the formula shown above, the power that is dissipated by a resistor can be easily calculated if we know what the differenceinpotential (d.d.p.) between the resistor terminals (U) as well as the electrical current established therein (i).
If we remember Ohm's 1st law, which states that electrical potential can be calculated by the product of electrical resistance (R), measured in ohms (Ω), by the electric current (i), in Amperes (A), it will be possible to write the dissipated power equation in three different shapes. Watch:
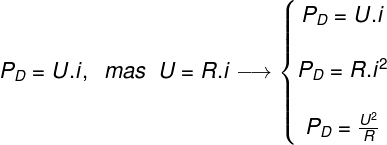
R – Resistance (Ω)
If we want to know the amount of energy that a resistor dissipated in a given period of time, we can use the expression shown below, check it out:
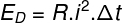
Exercises on power dissipated by resistors
1) When connected to a potential difference of 20 V, a resistor is carried by an electrical current of 0.5 A. In relation to this resistor, determine:
a) the power dissipated by it.
b) its electrical resistance.
Resolution:
a) To calculate the power dissipated by this resistor, we will use the following equation:

b) To calculate the electrical resistance of this resistor, we will use the formula below. Check out:
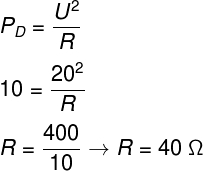
2) A resistor of constant electrical resistance equal to 10 Ω is traversed by an electrical current of 2 A, during a period of time of 60 minutes. Determine the amount of electrical energy dissipated by this resistor during this time span.
Resolution:
To solve the exercise, we will use the Joule law formula. Also, remember that the time interval used in this formula is defined in seconds, so you need to use the time of 3600 s instead of 60 minutes. Look:

By Me. Rafael Helerbrock
Source: Brazil School - https://brasilescola.uol.com.br/fisica/potencia-dissipada-num-resistor.htm
