Gas mixture. Dalton's law applied to gas mixture

Dalton's law states that the partial pressure of each gas in a gas mixture is equal to the pressure it would exert occupying the volume of the mixture, at the same temperature. Therefore, the total pressure of the gas mixture is the sum of the partial pressures of each gas that composes it.

Let's consider two types of gases, A and B. Each of them occupies the same volume V, and has the same temperature T. If we apply the Clapeyron equation to the two gases A and B, we have:

P_THE .V=n_THE .R .T and p_B .V=n_B .R .T

As shown in the figure above, if we mix the two gases, the number of moles of the gases in the mixture (no_m) it becomes:

no_m= n_THE+ n_B

Where:

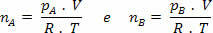
But nm = (Pm.V) / R. T; so we have:

Making some simplifications in the expression above, we have:

P_m=p_THE+ p_B (Dalton's Law)

We can apply the same reasoning to gases of different volumes and temperatures. Let's see the figure below, in which two balloons connected by a tube of negligible volume have a contact tap. These balloons have two gases A and B, with temperatures and volumes different from each other. From the figure we see that the faucet is closed, therefore:

P_THE .V=n_THE .R .T and p_B .V=n_B .R .T

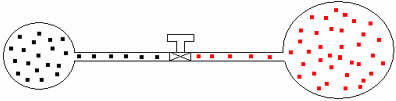
Later, if we open the faucet, we will see that the gases mix, as shown in the illustration below:

For this mixture, we have the following relationships:

V_m=V_THE+ V_B
P_THE .V=n_THE .R .T
P_B .V=n_B .R .T

So, we have that the final relationship of this mixture can be extended to a mixture of no gases. Thus:

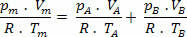
By Domitiano Marques
Graduated in Physics
Brazil School Team