When bodies are subjected to a variation in temperature they dilate, that is, they suffer an increase or decrease in their dimensions. It is worth noting that this variation is very small, and that it is often not perceptible to the naked eye, thus requiring equipment, such as a microscope, to be able to visualize it.
Bodies dilate when their temperature increases. It is known that when there is a variation in body temperature, the atoms that constitute it are more agitated, with this the average distance between them increases. Therefore, the body gains new dimensions, that is, it expands. Generally speaking, all bodies swell after being heated and contract after having their temperature reduced.
Linear expansion is that in which there is variation in only one dimension, that is, the length of the material. Imagine the following situation: a metal bar of length Li at temperature ti, is heated to a certain temperature tf. What can be seen is that the bar, after heating, is no longer the same length, that is, it has undergone a variation in its dimension, in its length, it has expanded. Look:
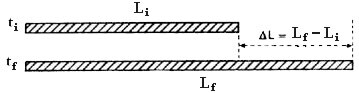
Where ΔL = Lf – Li is the variation in length, that is, the linear expansion of the bar. And Δt = tf – ti is the temperature variation of the bar. Experimentally it turns out that:
- the initial length (Li) is proportional to the initial temperature (ti);
- the final length (Lf) is proportional to the final temperature (tf);
- linear expansion depends on the material that makes up the bar.
Through these findings, the following equation for linear expansion of the bodies was determined: ΔL = Liα t, where α is called linear expansion coefficient, is a constant characteristic of the material that makes up the body. For example, for aluminum we have α = 0.000023 per °C (or °C-1), this means that aluminum dilates 23 millionths of its length at every 1°C of variation in its temperature, that is, a very small dilation that can possibly only be seen in microscope.
By Marco Aurélio da Silva
Source: Brazil School - https://brasilescola.uol.com.br/fisica/dilatacao-linear.htm
