You complex numbers arise from the need to resolve equations that have negative number root, which, until then, was not possible to solve by working with real numbers. Complex numbers can be represented in three ways: a algebraic form (z = a + bi), composed of a real part The and an imaginary part B; The Geometric form, represented in the complex plane also known as the Argand-Gauss plane; and yours trigonometric form, also known as the polar form. Based on their representation, as we are working with a numerical set, complex numbers have well-defined operations: addition, subtraction, multiplication, division and potentiation.
Through the geometric representation in the complex plane, we also define the module (represented by |z|) of a complex number — which is the distance from the point representing the complex number to the origin — and what is the argument of a complex number — which is the angle formed between the horizontal axis and the track that connects the origin to the point representing the number complex.
need for complex numbers
In mathematics, the expansion of a numerical set to a new set, throughout history, was something quite common. It so happens that, in the course of it, mathematics has developed, and then, to meet the needs of the time, it was noticed that there were numbers that did not belong to the numerical set to which it referred. It was like that with the emergence of numerical sets integers, rationals, irrationals and reals, and it was no different when there was a need to expand the set of real numbers to that of complex numbers.
When we try to solve quadratic equations, it is quite common that we find the square root of a negative number, which is impossible to be solved in the set of real numbers, hence the need for complex numbers. The beginning of the study of these numbers received contributions from important mathematicians, such as Giralmo Cardono, but their set was formalized by Gauss and Argand.
Read too: Geometric representation of the sum of complex numbers
Do not stop now... There's more after the advertising ;)
algebraic form of a complex number
When trying to solve a quadratic equation such as x² = –25, it was often said to be unsolvable. However, in an attempt to algebrize, the algebraic representation, which makes it possible to perform operations with these numbers, even though you cannot calculate the square root of a negative number.
To facilitate the resolution of situations in which you work with the square root of a negative number, the imaginary unit.

So, analyzing the equation presented x² = -25, we have that:
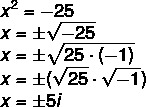
Thus, the solutions for the equation are -5i e5i.
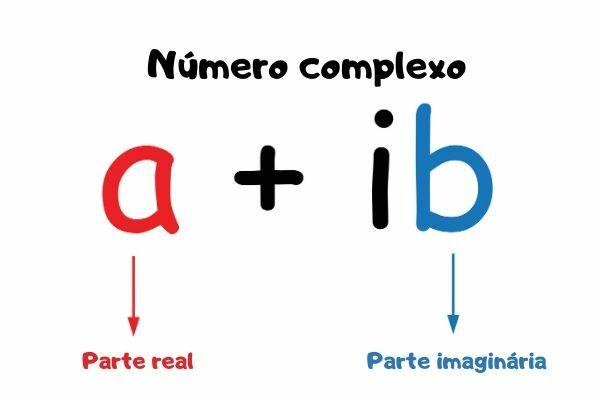
To define the algebraic form, the letter i, known as imaginary unit of a complex number. A complex number is represented by:
z = The + Bi
On what The and B are real numbers.
The: real part, indicated by a = Re (z);
B: imaginary part, indicated by Im (z);
i: imaginary unit.
Examples
The) 2 + 3i
B) -1 + 4i
ç) 5 – 0,2i
d) -1 – 3i
when the real part is null, the number is known as pure imaginary, for example, -5i and 5i they are pure imaginaries because they have no real part.
When the imaginary part is null, the complex number is also a real number.
Operations with complex numbers
Like any numerical set, the operations must be well defined, therefore, it is possible to perform the four basic operations of complex numbers taking into account the algebraic form presented.
Adding two complex numbers
To carry out the addition of two complex numbers z1 ez2, we'll add the real part of z1 ez2 and the sum of the imaginary part, respectively.
Be:
z1 = a + bi
z2 = c + di
z1 +z2 = (a + c) + (b + d)i
Example 1
Realization of the sum of z1 and z2.
z1 = 2 + 3i
z2 = 1 + 2i
z1 +z2= (2 + 1) + (3 + 2)i
z1 +z2= 3 + 5i
Example 2
Realization of the sum of z1 and z2.
z1 = 5 – 2i
z2 = – 3 + 2i
z1+z2 = (5 + (–3)) + (–2 + 2)i
z1+z2 = (5 – 3) + 0i
z1 +z2= 3 + 0i = 3
See too: Geometric representation of the sum of complex numbers
Subtraction of two complex numbers
Before we talk about subtraction, we need to define what is the inverse of a complex number, that is, z = a + bi. The inverse of z, represented by –z, is the complex number –z = –a –bi.
To perform the subtraction between z1and -z2, as well as in addition, we will do the subtraction between real parts and between imaginary parts separately, but it is necessary to understand that -z2 it is the inverse of a complex number, which makes it necessary to play the sign game.
Example 1
Performing the subtraction of z1 and z2.
z1 = 2 + 3i
z2 = 1 + 2i
z1–z2 = (2 – 1) + (3 – 2)i
z1–z2= 1 + 1i = 1+ i
Example 2
Performing the subtraction of z1 and z2.
z1= 5 – 2i
z2 = – 3 + 2i
z1–z2= (5 – (–3)) + (–2 – 2)i
z1–z2= (5 + 3) + (–4)i
z1 –z2= 8 + (–4)i
z1 –z2= 8 –4i
Imaginary Unit Powers
Before we talk about multiplication, we need to understand the power of the imaginary unit. In the search for a method to calculate powers of ino, it is necessary to realize that these powers behave in a cyclic way. For this, let's calculate some potencies in i.

It turns out that the next powers are nothing more than its repetition, note that:
i 4 = i 2 · i 2 = (–1) (–1) = 1
i 5 = i 2 · i 3 = (–1) (–i) = i
As we continue to calculate the powers, the answers will always be elements of the set {1,i,–1,–i}, then to find a power of the unit ino, we will divide n (the exponent) by 4, and the restof this division (r = { 0, 1, 2, 3}) will be the new exponent of i.
Example1
Calculation of i25
When we divide 25 by 4, the quotient will be 6 and the remainder will be equal to 1. So we have to:
i 25 = i1 = i
Example 2
Calculation of i 403
When we divide 403 by 4, the quotient will be 100, because 100 · 4 = 400, and the rest will be 3, so we have to:
i 403 =i 3 = -i
Multiplication of complex numbers
To perform the multiplication of two complex numbers, let's apply the distributive property. Be:
z1= a + bi
z2= c + di, then the product:
z1 · z2 = (a + bi) (c + di), applying the distributive property,
z1 · z2 = ac + adi + cbi + bdi 2, but as we've seen, i ² = -1
z1 · z2 = ac + adi + cbi – bd
z1 · z2= (ac – bd) + (ad + cb)i
Using this formula, it is possible to find the product of any two complex numbers, but in a In general, it does not need to be decorated, since, for the calculation in question, we just apply the property distributive.
Example
Calculation of the product of (2+3i) (1 – 4i):
(2+3i) (1 – 4i) = 2 – 8i + 3i– 12i ², remembering that i² = -1:
(2 + 3i) (1 – 4i) = 2 – 8i + 3i+ 12
(2 + 3i) (1 – 4i) = (2 + 12) + (– 8 + 3)i
(2+3i) (1 – 4i) = 14 – 5i
Also access: Complex number addition, subtraction and multiplication
Complex number conjugate
Before we talk about division, we need to understand what the conjugate of a complex number is. The concept is simple, to find the conjugate of a complex number, just to exchangemos the sign of the imaginary part.

division of two complex numbers
To carry out the division of two complex numbers, we need to multiply the fraction by the conjugate of the denominator so that what is the real part and what is the imaginary part is well defined.

Example
Calculation of division of (6 - 4i): (4 + 2i)

See too: Opposite, conjugate and equality of complex numbers
Complex plane or Argand-Gauss plane
Known as complex plan or A planrgand-gauss, he allows the representation in geometric form of a complex number, this plan is an adaptation in the Cartesian plane to represent complex numbers. The horizontal axis is known as real part axis Re(z), and the vertical axis is known as axis of the imaginary part Im (z). So the complex number represented by a + bi generates the points in the complex plane formed by the ordered pair (a, b).
Example
Representation of the number 3 + 2i in the geometric form Z(3,2).

Complex number modulo and argument
The modulus of a complex number, geometrically, is the distance from point (a, b) which represents this number in the complex plane to the origin, that is, the point (0,0).
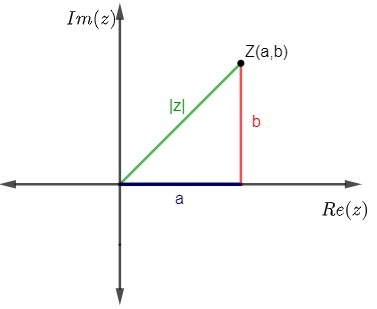
As we can see, |z| is the hypotenuse of right triangle, therefore, it can be calculated by applying the Pythagorean theorem, so we have to:

Example:
Calculation of the modulus of z = 1 + 3i
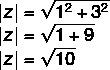
O Theargument of a complex number, geometrically, is the angle formed by the horizontal axis and the |z|

To find the angle value, we have to:

The goal is to find the angle θ = arg z.
Example:
Find the complex number argument: z = 2 + 2i:
Since a and b are positive, we know that this angle is in the first quadrant, so let's calculate |z|.

Knowing the |z|, it is possible to calculate the sine and the cosine.
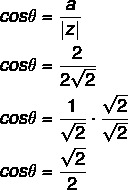
Since, in this case, a and b are equal to 2, then, when we calculate sinθ, we will find the same solution for the cosine.
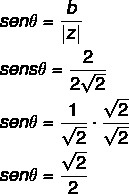
Knowing the values of sinθ and cosθ, when consulting the table of notable angles and knowing that θ belongs to the first quadrant, so θ can be found in degrees or radians, so we conclude what:
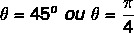
Trigonometric or polar form
The representation of the complex number in the trigonometric form it's only possible after we understand the concept of module and argument. Based on this representation, important concepts are developed for the study of complex numbers at a more advanced level. To perform the trigonometric representation, we will remember its algebraic form z = a + bi, however, when analyzing the complex plane, we have to:
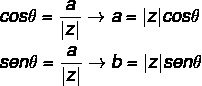
By substituting, in algebraic form, the values of a = |z| cos θ and b = |z| sen θ, we have to:
z = a + bi
With z = |z| cos θ + |z| senθ i, putting |z| in evidence, we arrive at the formula of the trigonometric form:
z= |z|(cos θ + i · sin θ) |
Example: Write, in trigonometric form, the number
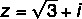
To write in trigonometric form, we need the argument and the modulus of z.
1st step – Calculation of |z|

Knowing the |z|, it is possible to find the value of θ by consulting the table of notable angles.

It is now possible to write the number z in its trigonometric form with the angle in degrees or with the angle measured in radians.
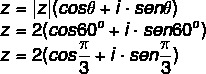
Read too: Radiation of complex numbers in trigonometric form
solved exercises
Question 1 - (UFRGS) Given the complex numbers z1 = (2,–1) and z2 = (3, x), it is known that the product between z1 and z2 is a real number. So x is equal to:
a) -6
b) -3/2
c) 0
d) 3/2
e) 6
Resolution
Alternative D.
For the product to be a real number, then the imaginary part is equal to zero.
By writing these numbers in algebraic form, we have to:
z1 = 2 – 1i and z2 = 3 + xi
z1 · z2 = (2 – 1i) (3 + xi)
z1 · z2 = 6 + 2xi –3i – xi ²
z1 · z2 = 6 + 2xi –3i + x
z1 · z2 = 6+ x + (2x – 3)i
Since our interest is that the imaginary part is equal to zero, then we will solve for 2x – 3 = 0
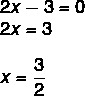
Question 2 - (UECE) If i is the complex number whose square is equal to -1, then the value of 5i 227 + i 6 – i 13 it's the same as:
The) i + 1
b) 4i –1
c) -6i –1
d) -6i
Resolution
Alternative C.
To solve this expression, it is necessary to find the remainder of each of the numbers in division by 4.
227: 4 results in quotient 56 and remainder 3.
i 227 = i 3 = –i
6: 4 results in quotient 1 and remainder 2.
i 6 = i 2 = –1
13: 4 results in quotient 3 and remainder 1.
i 13 = i1 = i
So we have to:
5i 227 + i 6 – i 13
5 (–i) + (–1) – i
–5i –1 – i
–6i – 1
By Raul Rodrigues de Oliveira
Maths teacher