In a 2nd degree equation, the resulting roots of mathematical operations depend on the value of the discriminant. The resulting situations are as follows:
∆ > 0, the equation has two different real roots.
∆ = 0, the equation has a single real root.
∆ < 0, the equation has no real roots.
In Mathematics, the discriminant of the 2nd degree equation is represented by the symbol ∆ (delta).
When the roots of this equation exist, in the format ax² + bx + c = 0, they will be calculated according to the mathematical expressions:
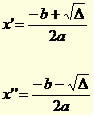
There is a relationship between the sum and the product of these roots, which is given by the following formulas:
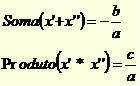
For example, in the 2nd degree equation x² – 7x + 10 = 0 we have that the coefficients hold: a = 1, b = – 7 and c = 10.
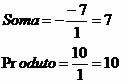
Based on these results, we can see that the roots of this equation are 2 and 5, since 2 + 5 = 7 and 2 * 5 = 10.
Take another example:
Let's determine the sum and product of the roots of the following equation: x² – 4x + 3 = 0.
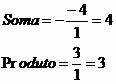
The roots of the equation are 1 and 3, since 1 + 3 = 4 and 1 * 3 = 3.
by Mark Noah
Graduated in Mathematics
Brazil School Team
Equation - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/relacao-das-raizes-equacao-2-grau.htm