Complex numbers are an extension of the set of real numbers. In fact, complex number is an ordered pair of real numbers (a, b). Written in normal form, the ordered pair (a, b) becomes z = a + bi. Representing this complex number in the Argand-Gauss plane, we will have:
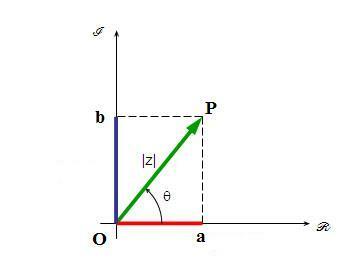
The line segment OP is called the modulus of the complex number. The arc formed between the positive horizontal axis and the counterclockwise segment OP is called the argument of z. Look at the figure below to determine the characteristics of the argument of z.
In the right triangle formed, we can say that:
We can also see that:
Or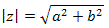
Example 1. Given the complex number z = 2 + 2i, determine the magnitude and argument of z.
Solution: From the complex number z = 2 + 2i, we know that a = 2 and b = 2. Follow that: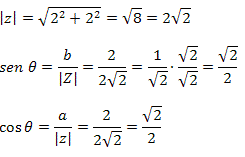
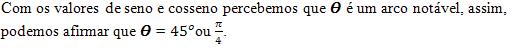
Example 2. Find the argument of the complex number z = – 3 – 4i.
Solution: To determine the argument of z, we need to know the value of |z|. Thus, as a = – 3 and b = – 4, we will have: 
In cases where the argument is not a notable angle, it is necessary to determine the value of its tangent, as done in the previous example, and only then can we say who the argument is.
Example 3. Given the complex number z = – 6i, determine the argument of z.
Solution: Let's calculate the modulus value of z.
By Marcelo Rigonatto
Specialist in Statistics and Mathematical Modeling
Brazil School Team
Complex numbers - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/argumento-um-numero-complexo.htm

