THE hyperbole is a flat geometric figure formed by the intersection between a flat it is a cone double of revolution. The figure resulting from this intersection it can also be defined algebraically, from the distance between two points. At hyperbole, although they are completely contained in a plane, they are curved. That means they don't have any flat parts.
The following image illustrates a hyperbola:

Formal definition of hyperbole
Given two points in the plane, F1 and F2, called focusesgiveshyperbole, and the distance 2c between them, the hyperbola is the setFrompoints whose difference in distances to F1 and until F2 is equal to a constant 2a.
In other words, P is a hyperbola point if |dPF1 – dPF2| = 2nd. The following figure exemplifies this definition. Note that the differenceof thedistances between the Q point and the foci is equal to the difference in the distance between the P point and the foci.
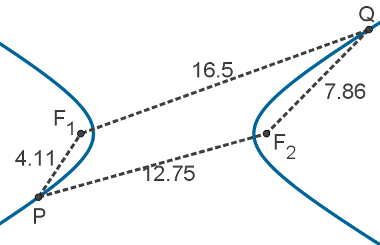
Hyperbole elements
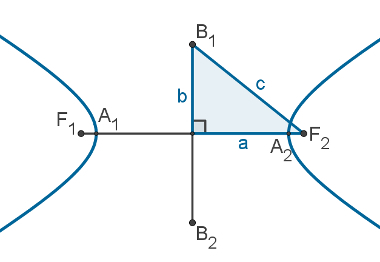
Spotlights: Are the F points1 and F2. THE distance between foci is 2c and is known as distancefocal.
center: Given the segment whose ends are the foci, the center of the hyperbola is the midpoint of this segment.
Axlereal: Hyperbola intersects segment F1F2 at points A1 and the2. segment A1THE2 is called the real axis. Actual shaft length is 2a.
Do not stop now... There's more after the advertising ;)
Axleimaginary: is the line segment B1B2perpendicular to the real axis, with Scoreaverage in the center of hyperbole. The distance from point B1 up to1 is equal to c, just like the distances from B1 the A2, B2 the A1 and B2 the A2. The length of the imaginary axis is 2b.
Eccentricity: is the reason to follow
ç
The
The following image shows the lengths “a”, “b” and “c” in a hyperbole, in which it is possible to observe the Pythagoras relation:
ç2 = the2 + b2
Reduced hyperbola equations
there are two equationsreduced gives hyperbole. The first is for the case where hyperbole has the focuses on the x-axis and center on the origin of a Cartesian plane:
x 2 – y 2 = 1
The2 B2
The second equation is for the case where hyperbola also has centeratorigin, but yours focuses are on the y axis of the Cartesian plane:
y 2 – x 2 = 1
The2 B2
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "What is hyperbole?"; Brazil School. Available in: https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-hiperbole.htm. Accessed on June 27, 2021.
slope, perpendicular lines, slope of perpendicular lines, condition of existence of perpendicular lines, tangent, inclination angle.


